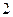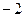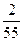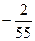题目内容
已知正方体ABCD-A1B1C1D1中,M、N分别为BB1、C1D1的中点,建立适当的坐标系,求平面AMN的法向量.
(-3,2,-4)为平面AMN的一个法向量.
以D为原点,DA、DC、DD1所在直线为坐标轴建立空间直角坐标系.(如图所示).

设棱长为1,则A(1,0,0),M(1,1, ),N(0,
),N(0, ,1).
,1).
∴ =(0,1,
=(0,1, ),
), =(-1,
=(-1, ,1).
,1).
设平面AMN的法向量n=(x,y,z)
∴
令y=2,∴x=-3,z=-4.∴n=(-3,2,-4).
∴(-3,2,-4)为平面AMN的一个法向量.

设棱长为1,则A(1,0,0),M(1,1,
 ),N(0,
),N(0, ,1).
,1).∴
 =(0,1,
=(0,1, ),
), =(-1,
=(-1, ,1).
,1).设平面AMN的法向量n=(x,y,z)
∴

令y=2,∴x=-3,z=-4.∴n=(-3,2,-4).
∴(-3,2,-4)为平面AMN的一个法向量.

练习册系列答案
相关题目
 的直径AB=3,点C为
的直径AB=3,点C为 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点. 平面VAC;
平面VAC;
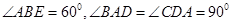 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.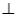 平面
平面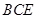 ;(2)点M在直线EF上,且
;(2)点M在直线EF上,且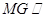 平面
平面 ,求平面ACH与平面ACM所成锐角的余弦值.
,求平面ACH与平面ACM所成锐角的余弦值.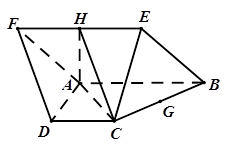
 A
A

 的菱形
的菱形 沿较短对角线
沿较短对角线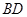 折成二面角
折成二面角 ,点
,点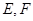 分别为
分别为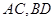 的中点,给出下列四个命题:
的中点,给出下列四个命题: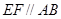 ;②
;②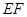 是异面直线
是异面直线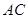 与
与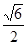 ;④
;④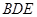 .
. 是边长为1的正方形,
是边长为1的正方形, 分别为
分别为 上的点,且
上的点,且 沿
沿 将正方形折成直二面角
将正方形折成直二面角 .
.
 平面
平面 ;
; 点
点 与平面
与平面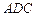 间的距离为
间的距离为 ,试用
,试用 表示
表示 ,
, ; (2)
; (2)  ,
, ;
; ,
, ; (4)
; (4) ,
,
 ,且
,且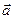 与
与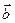 的夹角余弦为
的夹角余弦为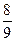 ,则
,则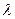 等于( )
等于( )