题目内容
已知正三棱锥
，点
都在半径为
的球面上，若
两两互相垂直，则球心到截面
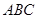的距离为________。
解析试题分析：设PA=PB=PC=
，则AB=AC=BC=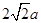
,设球半径为R=，所以
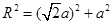，解得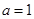
。所以三角形
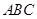是边长为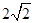
的正三角形，中线长为
。设球心到面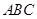的距离为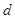
。因为球心在面ABC上的射影为三角形的中心，所以
，所以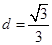
。
考点：怎样确定球心位置，点到面的距离
练习册系列答案
快乐5加2金卷系列答案
相关题目
快乐5加2金卷系列答案题目内容
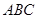已知正三棱锥，点都在半径为的球面上，若两两互相垂直，则球心到截面的距离为________。
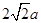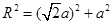解析试题分析：设PA=PB=PC=，则AB=AC=BC=,设球半径为R=，所以，解得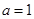。所以三角形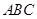是边长为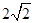的正三角形，中线长为。设球心到面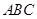的距离为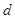。因为球心在面ABC上的射影为三角形的中心，所以，所以。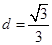
考点：怎样确定球心位置，点到面的距离
快乐5加2金卷系列答案
的底面边长
，若直线
与底面
所成的角的大小为
，则正四棱柱
是单位正方体
表面上的一个动点，且
。则
，
与平面
，
交于
两点。给出以下命题，其中真命题有________(写出所有正确命题的序号)
；
中点为
，
的中点为
，则直线
与面
有一个交点；
为
的内心；
为
的外心，则
为定值.