题目内容
有幂函数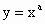 (a¹
0)若干个,每个函数至少具有下面三条性质之一:
(a¹
0)若干个,每个函数至少具有下面三条性质之一:
(1)是奇函数;(2)是(-¥ ,+¥ )内的增函数;(3)函数的图像经过原点.又已知同时具有性质(1)的共有15个,具有性质(2)的共有12个,具有性质(3)的共有18个.试问,这些幂函数共有几个?其中幂指数小于零的有几个?
答案:21,3
解析:
解析:
|
解:由幂数的性质知,在 (-¥ ,+¥ )内的增函数一定是奇函数,且图像一定过原点.又若一个幂函数是奇函数,且其图像又经过原点,则这个函数一定是在 (-¥ ,+¥ )上的增函数.设定些幂函数中分别具备性质 (1)(2)(3)的函数分别构成集合A、B、C,而幂指数小于零的构成集合D,依题意得card(A)=15,card(B)=12,card(C)=18, 又BÍ A,BÍ C,A∩CÍ B,BÍ A∩C, ∴A∩C=B. 则card(A∪B∪C)=card(A∪C)=card(A)+card(C)-card(A∩C)=card(A)+card(C)-card(B)=15+18-12=21. 即共有幂函数21个. 又幂指数小于零的幂函数图像一定不经过原点,反之亦然,故其中幂指数小于零的函数有21-18=3个. |

练习册系列答案
相关题目
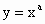 (a¹
0)若干个,每个函数至少具有下面三条性质之一:
(a¹
0)若干个,每个函数至少具有下面三条性质之一: