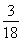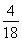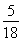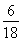题目内容
甲从正方形四个顶点中任意选择两个顶点连成直线，乙从该正方形四个顶点中任意选择两个顶点连成直线，则所得的两条直线相互垂直的概率是
．
| 5 |
| 18 |
| 5 |
| 18 |
分析：由题意知本题是一个古典概型，本题所包含的总事件数正方形四个顶点可以确定6条直线，甲乙各自任选一条共有36个基本事件．4组邻边和对角线中两条直线相互垂直的情况有5种包括10个基本事件，根据古典概型公式得到结果．
解答：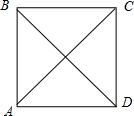
解：正方形四个顶点可以确定6条直线，
甲乙各自任选一条共有36个基本事件．
4组邻边和对角线中两条直线相互垂直的情况有5种
包括10个基本事件，即AB与BC，AB与AD，BC与BA，BC与CD，CD与BC，CD与AD，AD与CD，AD与AB，AC与BD，BD与AC．
所以概率P=
=
，
故答案为
．
解：正方形四个顶点可以确定6条直线，甲乙各自任选一条共有36个基本事件．
4组邻边和对角线中两条直线相互垂直的情况有5种
包括10个基本事件，即AB与BC，AB与AD，BC与BA，BC与CD，CD与BC，CD与AD，AD与CD，AD与AB，AC与BD，BD与AC．
所以概率P=
| 10 |
| 36 |
| 5 |
| 18 |
故答案为
| 5 |
| 18 |
点评：对于几何中的概率问题，关键是正确理解几何图形，分类得出基本事件数，然后得所求事件的基本事件数，进而利用概率公式求概率．
练习册系列答案
轻松暑假总复习系列答案
相关题目
甲从正方形四个顶点中任意选择两个顶点连成直线，乙从该正方形四个顶点中任意选择两个顶点连成直线，则所得的两条直线相互垂直的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
（A）
（A）
（A）
（A）
（A）
（A）
