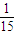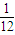题目内容
盒子中放有编号为1,2,3,4,5的形状和大小完全相同的5个白球和5个黑球,从中任意取出3个,则取出球的编号互不相同的概率为
- A.

- B.

- C.

- D.

D
分析:根据题意,先由组合数公式计算从10个球中取出3个的取法数目,若取出的球的编号互不相同,可以先从5个编号中选取3个编号,对于每一个编号,再选择球的颜色,由分步计数原理可得取出的球的编号互不相同的取法数目,由古典概型公式,计算可得答案.
解答:根据题意,盒子中共有10个球,从中任意取出3个,有C103=120种取法,
若取出的3个球编号互不相同,可先从5个编号中选取3个编号,有C53种选法.
对于每一个编号,再选择球,有两种颜色可供挑选,共有23种选法,
取出的球的编号互不相同的取法有C53•23=80种,
则取出球的编号互不相同的概率P= =
= ;
;
故选D.
点评:本题考查等可能事件的概率计算与排列、组合的应用,难点是由分步计数原理计算得到“取出球的编号互不相同”的取法数目.
分析:根据题意,先由组合数公式计算从10个球中取出3个的取法数目,若取出的球的编号互不相同,可以先从5个编号中选取3个编号,对于每一个编号,再选择球的颜色,由分步计数原理可得取出的球的编号互不相同的取法数目,由古典概型公式,计算可得答案.
解答:根据题意,盒子中共有10个球,从中任意取出3个,有C103=120种取法,
若取出的3个球编号互不相同,可先从5个编号中选取3个编号,有C53种选法.
对于每一个编号,再选择球,有两种颜色可供挑选,共有23种选法,
取出的球的编号互不相同的取法有C53•23=80种,
则取出球的编号互不相同的概率P=
 =
= ;
;故选D.
点评:本题考查等可能事件的概率计算与排列、组合的应用,难点是由分步计数原理计算得到“取出球的编号互不相同”的取法数目.

练习册系列答案
相关题目