题目内容
曲线C1,C2都是以原点O为对称中心、离心率相等的椭圆.点M的坐标是(0,1),线段MN是C1的短轴,是C2的长轴.直线l:y=m(0<m<1)与C1交于A,D两点(A在D的左侧),与C2交于B,C两点(B在C的左侧).(Ⅰ)当m=
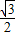 ,
,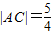 时,求椭圆C1,C2的方程;
时,求椭圆C1,C2的方程;(Ⅱ)若OB∥AN,求离心率e的取值范围.
【答案】分析:(Ⅰ)可设C1的方程为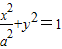 ,C2的方程为
,C2的方程为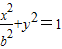 ,其中a>1,0<b<1,由C1,C2的离心率相同,可建立关于a,b的方程,结合
,其中a>1,0<b<1,由C1,C2的离心率相同,可建立关于a,b的方程,结合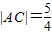 ,可求a,b进而可求椭圆C1,C2的方程
,可求a,b进而可求椭圆C1,C2的方程
(Ⅱ)由OB∥AN,可得kOB=kAN,从而可得m,a的关系,代入可由离心率表示a,进而可由离心率e表示m,结合m的范围可求e的范围
解答:解:(Ⅰ)设C1的方程为 ,C2的方程为
,C2的方程为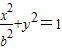 ,其中a>1,0<b<1…(2分)
,其中a>1,0<b<1…(2分)
∵C1,C2的离心率相同,所以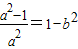 ,
,
所以ab=1,….…(3分)
∴C2的方程为a2x2+y2=1.
当m=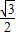 时,A
时,A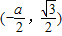 ,C
,C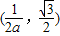 ….(5分)
….(5分)
又∵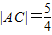 ,所以,
,所以,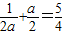 ,解得a=2或a=
,解得a=2或a= (舍),….…..(6分)
(舍),….…..(6分)
∴C1,C2的方程分别为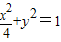 ,4x2+y2=1.….(7分)
,4x2+y2=1.….(7分)
(Ⅱ)A(-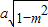 ,m),B(-
,m),B(- ,m). …(9分)
,m). …(9分)
∵OB∥AN,∴kOB=kAN,
∴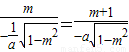 ,
,
∴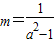 . ….(11分)
. ….(11分)
 ,
,
∴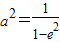 ,
,
∴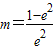 . …(12分)
. …(12分)
∵0<m<1,
∴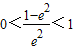 ,
,
∴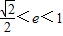 …(13分)
…(13分)
点评:本题主要考查了由椭圆的性质求解椭圆方程,及椭圆性质的综合应用,解答本题要求考生具备综合运用知识的能力
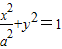 ,C2的方程为
,C2的方程为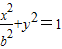 ,其中a>1,0<b<1,由C1,C2的离心率相同,可建立关于a,b的方程,结合
,其中a>1,0<b<1,由C1,C2的离心率相同,可建立关于a,b的方程,结合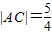 ,可求a,b进而可求椭圆C1,C2的方程
,可求a,b进而可求椭圆C1,C2的方程(Ⅱ)由OB∥AN,可得kOB=kAN,从而可得m,a的关系,代入可由离心率表示a,进而可由离心率e表示m,结合m的范围可求e的范围
解答:解:(Ⅰ)设C1的方程为
 ,C2的方程为
,C2的方程为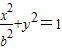 ,其中a>1,0<b<1…(2分)
,其中a>1,0<b<1…(2分)∵C1,C2的离心率相同,所以
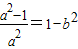 ,
,所以ab=1,….…(3分)
∴C2的方程为a2x2+y2=1.
当m=
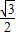 时,A
时,A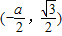 ,C
,C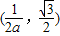 ….(5分)
….(5分)又∵
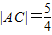 ,所以,
,所以,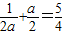 ,解得a=2或a=
,解得a=2或a= (舍),….…..(6分)
(舍),….…..(6分)∴C1,C2的方程分别为
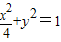 ,4x2+y2=1.….(7分)
,4x2+y2=1.….(7分)(Ⅱ)A(-
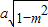 ,m),B(-
,m),B(- ,m). …(9分)
,m). …(9分)∵OB∥AN,∴kOB=kAN,
∴
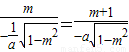 ,
,∴
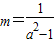 . ….(11分)
. ….(11分) ,
,∴
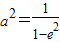 ,
,∴
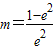 . …(12分)
. …(12分)∵0<m<1,
∴
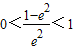 ,
,∴
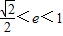 …(13分)
…(13分)点评:本题主要考查了由椭圆的性质求解椭圆方程,及椭圆性质的综合应用,解答本题要求考生具备综合运用知识的能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
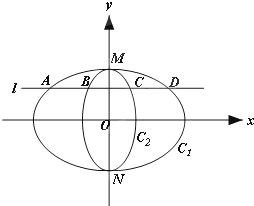 如图,曲线C1,C2都是以原点O为对称中心、离心率均为e的椭圆.线段MN是C1的短轴,是C2的长轴,其中M点坐标为(0,1),直线l:y=m,(0<m<1)与C1交于A,D两点,与C2交于B,C两点.
如图,曲线C1,C2都是以原点O为对称中心、离心率均为e的椭圆.线段MN是C1的短轴,是C2的长轴,其中M点坐标为(0,1),直线l:y=m,(0<m<1)与C1交于A,D两点,与C2交于B,C两点. ,
,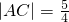 时,求椭圆C1,C2的方程;
时,求椭圆C1,C2的方程;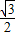 ,
,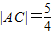 时,求椭圆C1,C2的方程;
时,求椭圆C1,C2的方程;