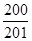题目内容
正项数列{an}的前n项和Sn满足：
－(n2＋n－1)Sn－(n2＋n)＝0.
(1)求数列{an}的通项公式an；
(2)令bn＝
，数列{bn}的前n项和为Tn，证明：对于任意的n∈N*，都有Tn<
.
－(n2＋n－1)Sn－(n2＋n)＝0.(1)求数列{an}的通项公式an；
(2)令bn＝
，数列{bn}的前n项和为Tn，证明：对于任意的n∈N*，都有Tn<.（1）an＝2n（2）
(1)由－(n2＋n－1)Sn－(n2＋n)＝0，得[Sn－(n2＋n)](Sn＋1)＝0，由于{an}是正项数列，所以Sn＋1>0.所以Sn＝n2＋n.n≥2时，an＝Sn－Sn－1＝2n，n＝1时，a1＝S1＝2适合上式．∴an＝2n.
(2)由an＝2n，得
bn＝
＝
Tn＝
＝
<
＝
－(n2＋n－1)Sn－(n2＋n)＝0，得[Sn－(n2＋n)](Sn＋1)＝0，由于{an}是正项数列，所以Sn＋1>0.所以Sn＝n2＋n.n≥2时，an＝Sn－Sn－1＝2n，n＝1时，a1＝S1＝2适合上式．∴an＝2n.(2)由an＝2n，得
bn＝
＝Tn＝
＝
<＝
练习册系列答案
相关题目
－y2＝1的右焦点为F，点P1、P2、…、Pn是其右上方一段(2≤x≤2 
，y≥0)上的点，线段|PkF|的长度为ak(k＝1,2,3，…，n)．若数列{an}成等差数列且公差d∈
，则n的最大取值为________．
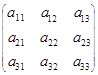中，每行的3个数依次成等差数列，每列的3个数也依次成等差数列，若
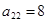，则这9个数的和为( )
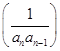的前200项和为 ( )．
