题目内容
设函数![]()
(I) 若x=2是函数f(x)的极值点,1和![]() 是函数
是函数![]() 的两个不同零点,且
的两个不同零点,且![]() ,求
,求![]() 。
。
(II) 若对任意![]() , 都存在
, 都存在![]() (e 为自然对数的底数),使得
(e 为自然对数的底数),使得![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
(Ⅰ)![]() ,∵
,∵![]() 是函数
是函数![]() 的极值点,∴
的极值点,∴![]() .∵1是函数
.∵1是函数![]() 的零点,得
的零点,得![]() ,
,
由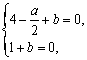 解得
解得![]() . ………2分
. ………2分
∴![]() ,
,![]() ,
,
令![]() ,
,![]() ,得
,得![]() ; 令
; 令![]() 得
得![]() ,
,
所以![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增.……4分
上单调递增.……4分
故函数![]() 至多有两个零点,其中
至多有两个零点,其中![]()
![]() ,
,
因为![]() ,
,![]()
![]() ,所以
,所以![]() ,故
,故![]() .……6分
.……6分
(Ⅱ)令![]() ,
,![]() ,则
,则![]() 为关于
为关于![]() 的一次函数且为增函数,根据题意,对任意
的一次函数且为增函数,根据题意,对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,则
成立,则![]() 在
在![]() 有解,
有解,
令![]() ,只需存在
,只需存在![]() 使得
使得![]() 即可,
即可,
由于![]() =
=![]() ,
,
令![]() ,
,![]() ,
,
∴![]() 在(1,e)上单调递增,
在(1,e)上单调递增,![]() ,………9分
,………9分
①当![]() ,即
,即![]() 时,
时,![]() ,即
,即![]() ,
,![]() 在(1,e)上单调递增,∴
在(1,e)上单调递增,∴![]() ,不符合题意.
,不符合题意.
②当![]() ,即
,即![]() 时,
时,![]() ,
,![]()
若![]() ,则
,则![]() ,所以在(1,e)上
,所以在(1,e)上![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() 在(1,e)上单调递减,
在(1,e)上单调递减,


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目