题目内容
某同学在研究函数y=f(x)(x≥1,x∈N)的性质,他已经正确地证明了函数f(x)满足:f(3x)=3f(x),并且当1≤x≤3时,f(x)=[1-|x-2|],这样对任意x≥1,他都可以求f(x)的值了,比如f(3×
 )=3f(
)=3f( )=3[1-|
)=3[1-| -2|]=1,f(54)=33f(
-2|]=1,f(54)=33f( )=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 .
)=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 .
【答案】分析:由f(3x)=3f(x)将f(99)递推下去求得18,再利用f(3x)=3f(x)递推得到f(x)=33f(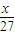 )=27[1-|
)=27[1-|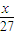 -2|]=18,然后分类讨论去绝对值求解.
-2|]=18,然后分类讨论去绝对值求解.
解答:解:根据题意:f(99)=3f(33)=32f(11)=33f(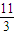 )=34f(
)=34f(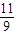 )=81[1-|
)=81[1-|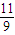 -2|]=18
-2|]=18
∴f(x)=33f(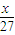 )=27[1-|
)=27[1-|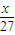 -2|]=18
-2|]=18
当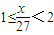 时,27×[
时,27×[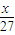 -1]=18解得:x=45
-1]=18解得:x=45
当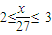 时,27×[3-
时,27×[3-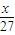 ]=18解得x=63
]=18解得x=63
∴集合M={x|f(x)=f(99)}中最小的元素是 45
故答案为:45
点评:本题是一定义题,要严格按照题目要求转化为已知的问题去解决,本题涉及到定义及绝对值方程的求法.
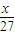 )=27[1-|
)=27[1-|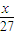 -2|]=18,然后分类讨论去绝对值求解.
-2|]=18,然后分类讨论去绝对值求解.解答:解:根据题意:f(99)=3f(33)=32f(11)=33f(
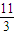 )=34f(
)=34f(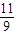 )=81[1-|
)=81[1-|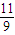 -2|]=18
-2|]=18∴f(x)=33f(
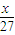 )=27[1-|
)=27[1-|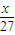 -2|]=18
-2|]=18当
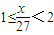 时,27×[
时,27×[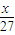 -1]=18解得:x=45
-1]=18解得:x=45当
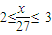 时,27×[3-
时,27×[3-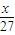 ]=18解得x=63
]=18解得x=63∴集合M={x|f(x)=f(99)}中最小的元素是 45
故答案为:45
点评:本题是一定义题,要严格按照题目要求转化为已知的问题去解决,本题涉及到定义及绝对值方程的求法.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 )=3f(
)=3f( )=3[1-|
)=3[1-| -2|]=1,f(54)=33f(
-2|]=1,f(54)=33f( )=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 .
)=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 . )=3f(
)=3f( )=3[1-|
)=3[1-| -2|]=1,f(54)=33f(
-2|]=1,f(54)=33f( )=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 .
)=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 .