题目内容

（2009•襄阳模拟）已知向量
a
=（1，n），
b
=（-1，n），若
a
与
b
垂直，则|
a
|等于（　　）
分析：利用向量垂直的充要条件：数量积为0得到-1+n2=0，所以n=±1，得到
a
=（1，±1），利用向量模的坐标公式进而求出|
a
|的值．
解答：解：因为向量
a
=（1，n），
b
=（-1，n），并且
a
与
b
垂直，
所以
a
•
b
=0
所以-1+n2=0，
解得n=±1，
所以
a
=
1+ (±1)2
=（1，±1）
所以|
a
|=
2

故选C．
点评：本题考查向量垂直的充要条件以及向量的求模的计算公式，此题属于基础题．
练习册系列答案
相关题目
（2009•襄阳模拟）过点A（2，-3），且与向量m=（4，-3）垂直的直线方程是
4x-3y-17=0
4x-3y-17=0
．
（2009•襄阳模拟）已知数列{an}的前n项和Sn是二项式（1+2x）2n（n∈N* ）展开式中含x奇次幂的系数和．
（1）求数列{an}的通项公式；
（2）设f（n）=
4
9an+12
，求f（0）+f（
1
n
）+f（
2
n
）+…+f（
n
n
）；
（3）证明：
a2
(a2-4)(a3-4)
+
a3
(a3-4)(a4-4)
+…+
an
(an-4)(an+1-4)
≥
1
256
（1-
1
4n2-3n
）．
（2009•襄阳模拟）将函数f（x）=2x+1-1的反函数的图象按向量
a
=（1，1）平移后得到函数g（x）的图象，则g （x）的表达式为（　　）
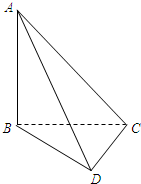（2009•襄阳模拟）在如图所示的四面体ABCD中，AB、BC、CD两两互相垂直，且BC=CD=1．
（1）求证：平面ACD⊥平面ABC；
（2）求二面角C-AB-D的大小；
（3）若直线BD与平面ACD所成的角为θ，求θ的取值范围．
（2009•襄阳模拟）设全集U={1，3，5，7}，M={1，a-5}，CUM={5，7}，则实数a的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网