题目内容
若ξ~N(0,1),且令Φ(x)=P(ξ≤x,x>0),则下列等式中成立的个数( )
①Φ(-x)=1-Φ(x);
②P{|ξ|≤x}=1-2Φ(x);
③P{|ξ|<x}=2Φ(x)-1;
④P{|ξ|>x}=2[1-Φ(x)].
①Φ(-x)=1-Φ(x);
②P{|ξ|≤x}=1-2Φ(x);
③P{|ξ|<x}=2Φ(x)-1;
④P{|ξ|>x}=2[1-Φ(x)].
分析:根据随机变量ξ服从标准正态分布N(0,1),得到正态曲线关于ξ=0对称,再结合正态分布的密度曲线定义Φ(x)=P(ξ≤x,x>0),由此可解决问题.
解答: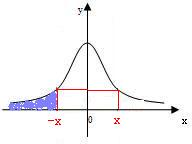 解:∵随机变量ξ服从标准正态分布N(0,1),
解:∵随机变量ξ服从标准正态分布N(0,1),
∴正态曲线关于ξ=0对称,
∵Φ(x)=P(ξ≤x,x>0),根据曲线的对称性可得:
①Φ(-x)=1-Φ(x)正确;
②P{|ξ|≤x}=1-2Φ(x)正确;
③P{|ξ|<x}=2Φ(x)-1错误;
④P{|ξ|>x}=2[1-Φ(x)]正确.
故选C.
 解:∵随机变量ξ服从标准正态分布N(0,1),
解:∵随机变量ξ服从标准正态分布N(0,1),∴正态曲线关于ξ=0对称,
∵Φ(x)=P(ξ≤x,x>0),根据曲线的对称性可得:
①Φ(-x)=1-Φ(x)正确;
②P{|ξ|≤x}=1-2Φ(x)正确;
③P{|ξ|<x}=2Φ(x)-1错误;
④P{|ξ|>x}=2[1-Φ(x)]正确.
故选C.
点评:本题考查正态分布曲线的特点及曲线所表示的意义,标准正态总体在任一区间(a,b)内取值概率P(a<ξ<b)=∅(b)-∅(a),本题属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
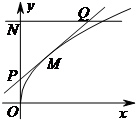 如图为函数
如图为函数