题目内容
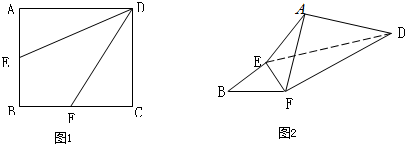 正方形ABCD(图1)中,AB=2,E、F分别是边AB及BC的中点,将△AED及△DCF折起(如图2),使A、C点重合于A'点.
正方形ABCD(图1)中,AB=2,E、F分别是边AB及BC的中点,将△AED及△DCF折起(如图2),使A、C点重合于A'点.(1)证明:A′D⊥EF;
(2)证明:平面A′FD⊥平面A′ED;
(3)求A′D与平面DEF所成角的正切值.
分析:(1)由折叠前后的角度不变得到A′D⊥A′E,A′D⊥A′F,然后利用线面垂直的判定得到A′D⊥面A′EF,从而得到答案;
(2)要证平面A′FD⊥平面A′ED,只要证明平面A′FD经过面A′ED的一条垂线A′F即可,利用△BEF≌△A′EF得到A′E⊥A′F,结合(1)可证得结论;
(3)先证出面A′OD⊥面DEF,然后找出线面角,通过解直角三角形求解A′D与平面DEF所成角的正切值.
(2)要证平面A′FD⊥平面A′ED,只要证明平面A′FD经过面A′ED的一条垂线A′F即可,利用△BEF≌△A′EF得到A′E⊥A′F,结合(1)可证得结论;
(3)先证出面A′OD⊥面DEF,然后找出线面角,通过解直角三角形求解A′D与平面DEF所成角的正切值.
解答: (1)证明:∵ABCD是正方形,而折叠前后的角度不变,
(1)证明:∵ABCD是正方形,而折叠前后的角度不变,
∴A′D⊥A′E,A′D⊥A′F,
由
⇒A′D⊥面A′EF⇒A′D⊥EF;
(2)证明:∵BE=A′E,BF=A′F,EF=EF.
∴△BEF≌△A′EF,
∵∠EBF=90°,
∴A′E⊥A′F,
又由(1)知A′F⊥A′D,
A′D∩A′E=A′.
∴A′F⊥面A′ED⇒面A′FD⊥面A′ED;
(3)解:设BD∩EF=O,则O为EF中点,且EF⊥BD.
∴
⇒EF⊥面A′OD⇒面A′OD⊥面DEF,
作A′H⊥OD于H,则A′H⊥面DEF,
∴∠A′DH为A′D与面DEF所成的角且等于∠A′DO,
在Rt△A′OD中,A′D=2,A′O=BO=
,
∴tan∠A′DO=
=
.
 (1)证明:∵ABCD是正方形,而折叠前后的角度不变,
(1)证明:∵ABCD是正方形,而折叠前后的角度不变,∴A′D⊥A′E,A′D⊥A′F,
由
|
(2)证明:∵BE=A′E,BF=A′F,EF=EF.
∴△BEF≌△A′EF,
∵∠EBF=90°,
∴A′E⊥A′F,
又由(1)知A′F⊥A′D,
A′D∩A′E=A′.
∴A′F⊥面A′ED⇒面A′FD⊥面A′ED;
(3)解:设BD∩EF=O,则O为EF中点,且EF⊥BD.
∴
|
作A′H⊥OD于H,则A′H⊥面DEF,
∴∠A′DH为A′D与面DEF所成的角且等于∠A′DO,
在Rt△A′OD中,A′D=2,A′O=BO=
| ||
| 2 |
∴tan∠A′DO=
| A′O |
| A′D |
| ||
| 4 |
点评:本题考查了直线与直线处置的判定,考查了直线与平面垂直的判定和性质,解答该题的关键在于明确折叠前后的变量和不变量,是中档题.

练习册系列答案
相关题目
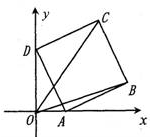 如图放置的正方形ABCD,AB=1,A,D分别在x,y轴的正半轴上(含坐标原点)滑动,则
如图放置的正方形ABCD,AB=1,A,D分别在x,y轴的正半轴上(含坐标原点)滑动,则 如图,边长为4的正方形ABCD中
如图,边长为4的正方形ABCD中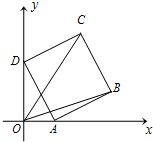 (2013•临沂三模)如图放置的正方形ABCD,AB=1,A,D分别在x轴、y轴的正半轴(含原点)上滑动,则
(2013•临沂三模)如图放置的正方形ABCD,AB=1,A,D分别在x轴、y轴的正半轴(含原点)上滑动,则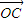 •
•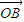 的最大值是 .
的最大值是 .