题目内容
 已知函数
已知函数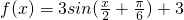
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)求出f(x)的周期、单调增区间;
(3)说明此函数图象可由y=sinx的图象经怎样的变换得到.
解:(1)列表:
作图:
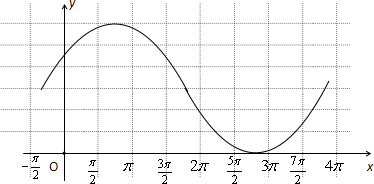
(2)由图象可得 周期T=4π,由 2kπ- ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,可得 4kπ-
,k∈z,可得 4kπ- ≤x≤4kπ+
≤x≤4kπ+ ,
,
故单调增区间为[4kπ- ,4kπ+
,4kπ+ ],k∈z.
],k∈z.
(3)把y=sinx的图象向左平移 个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),
个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),
再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin( )+3
)+3
的图象.
分析:(1)列表,令 分别等于0,
分别等于0, ,π,
,π, ,2π,求得对应的x,y值,以这五对x,y值作为点的坐标,在坐标系中描出,用平滑曲线连接,即得它在一个周期内的闭区间上的图象.
,2π,求得对应的x,y值,以这五对x,y值作为点的坐标,在坐标系中描出,用平滑曲线连接,即得它在一个周期内的闭区间上的图象.
(2)根据图象写出周期,由 2kπ- ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即得单调增区间.
,k∈z,求得x的范围,即得单调增区间.
(3)把y=sinx的图象向左平移 个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin(
个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin(  )+3
)+3
的图象.
点评:本题考查用五点法作y=Asin(ωx+∅)+b的图象,以及此函数的性质、图象变换,用五点法作y=Asin(ωx+∅)+b的图象,是解题的关键.
 | 0 |  | π |  | 2 π |
| x | - |  |  | 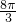 | 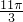 |
| y=3sin(2x+)+3 | 3 | 6 | 3 | 0 | 3 |

(2)由图象可得 周期T=4π,由 2kπ-
 ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,可得 4kπ-
,k∈z,可得 4kπ- ≤x≤4kπ+
≤x≤4kπ+ ,
,故单调增区间为[4kπ-
 ,4kπ+
,4kπ+ ],k∈z.
],k∈z.(3)把y=sinx的图象向左平移
 个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),
个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin(
 )+3
)+3的图象.
分析:(1)列表,令
 分别等于0,
分别等于0, ,π,
,π, ,2π,求得对应的x,y值,以这五对x,y值作为点的坐标,在坐标系中描出,用平滑曲线连接,即得它在一个周期内的闭区间上的图象.
,2π,求得对应的x,y值,以这五对x,y值作为点的坐标,在坐标系中描出,用平滑曲线连接,即得它在一个周期内的闭区间上的图象.(2)根据图象写出周期,由 2kπ-
 ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即得单调增区间.
,k∈z,求得x的范围,即得单调增区间.(3)把y=sinx的图象向左平移
 个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin(
个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin(  )+3
)+3的图象.
点评:本题考查用五点法作y=Asin(ωx+∅)+b的图象,以及此函数的性质、图象变换,用五点法作y=Asin(ωx+∅)+b的图象,是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

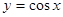 图象经过怎样的变换可以得到
图象经过怎样的变换可以得到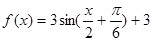
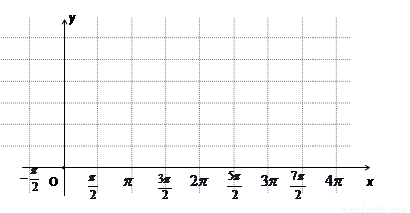
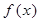 的单调增区间;
的单调增区间;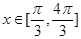 ,求
,求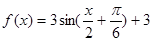
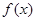 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;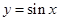 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.
 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴; 上的图象经怎样的变换得到
上的图象经怎样的变换得到 .
.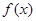 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;