题目内容
河上有一抛物线型拱桥,当水面距拱顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高 m,问水面上涨到与抛物线拱顶相距 m时,小船不能通航.
m,问水面上涨到与抛物线拱顶相距 m时,小船不能通航.
【答案】分析:先建立直角坐标系,设抛物线的标准方程,将点(4,-5)代入求得p,得到抛物线方程.再把点(2,y1)求得y1,进而求得 +|y1|得到答案.
+|y1|得到答案.
解答:解:建立直角坐标系,设抛物线方程为x2=-2py(p>0).
将点(4,-5)代入求得p=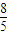 .
.
∴x2=-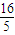 y.
y.
将点(2,y1)代入方程求得y1=- .
.
∴ +|y1|=
+|y1|= +
+ =2(m),
=2(m),
故答案为2.
点评:本题主要考查了抛物线的应用.在实际应用中常需要先建立直角坐标系,设出标准方程,根据题设条件求得方程,达到解决问题的目的.
 +|y1|得到答案.
+|y1|得到答案.解答:解:建立直角坐标系,设抛物线方程为x2=-2py(p>0).
将点(4,-5)代入求得p=
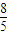 .
.∴x2=-
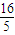 y.
y.将点(2,y1)代入方程求得y1=-
 .
.∴
 +|y1|=
+|y1|= +
+ =2(m),
=2(m),故答案为2.
点评:本题主要考查了抛物线的应用.在实际应用中常需要先建立直角坐标系,设出标准方程,根据题设条件求得方程,达到解决问题的目的.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 时,水面宽为8
时,水面宽为8

 m,问水面上涨到与抛物线拱顶相距 m时,小船不能通航.
m,问水面上涨到与抛物线拱顶相距 m时,小船不能通航. m,问水面上涨到与抛物线拱顶相距 m时,小船不能通航.
m,问水面上涨到与抛物线拱顶相距 m时,小船不能通航.