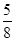题目内容
已知数列![]() 的首项
的首项![]() (a是常数,且
(a是常数,且![]() ),
),![]() (
(![]() ),数列
),数列![]() 的首项
的首项![]() ,
,![]() (
(![]() )。
)。
(1)证明:![]() 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设![]() 为数列
为数列![]() 的前n项和,且
的前n项和,且![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)当a>0时,求数列![]() 的最小项。
的最小项。
解:(1)∵![]()
∴![]()
![]() (n≥2)
(n≥2)
由![]() 得
得![]() ,
,![]() ,
,
∵![]() ,∴
,∴ ![]() ,
,
即![]() 从第2项起是以2为公比的等比数列。
从第2项起是以2为公比的等比数列。
(2)![]()
当n≥2时,![]()
∵![]() 是等比数列, ∴
是等比数列, ∴![]() (n≥2)是常数,
(n≥2)是常数,
∴3a+4=0,即![]() 。
。
(3)由(1)知当![]() 时,
时,![]() ,
,
所以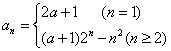 ,
,
所以数列![]() 为2a+1,4a,8a-1,16a,32a+7,……
为2a+1,4a,8a-1,16a,32a+7,……
显然最小项是前三项中的一项。
当![]() 时,最小项为8a-1;
时,最小项为8a-1;
当![]() 时,最小项为4a或8a-1;
时,最小项为4a或8a-1;
当![]() 时,最小项为4a;
时,最小项为4a;
当![]() 时,最小项为4a或2a+1;
时,最小项为4a或2a+1;
当![]() 时,最小项为2a+1。
时,最小项为2a+1。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
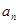 }的首项
}的首项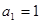 ,
,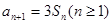 ,则下列结论正确的是( )
,则下列结论正确的是( )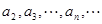 是等比数列 B.数列{
是等比数列 B.数列{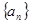 的首项
的首项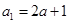 (a是常数,且
(a是常数,且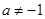 ),
),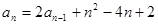 (
(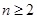 ),数列
),数列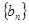 的首项
的首项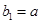 ,
,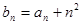 (
(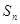 为数列
为数列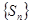 是等比数列,求实数
是等比数列,求实数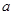 的值;
的值;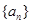 的首项
的首项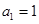 ,且满足
,且满足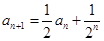 ,则此数列的第四项是
,则此数列的第四项是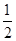 B
B 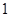 C
C 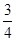 D
D