题目内容
(1)求经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上圆方程;
(2)设圆上的点A(2,3)关于直线x+2y=0的对称点仍在这个圆上,且与直线x-y+1=0相交的弦长为![]() ,求圆方程。
,求圆方程。
命题意图![]() 本题主要考查圆的方程的表达形式及对称性的问题,可利用数形结合法,利用圆中“半径、半弦、弦心距”构成直角三角形可解.
本题主要考查圆的方程的表达形式及对称性的问题,可利用数形结合法,利用圆中“半径、半弦、弦心距”构成直角三角形可解.
知识依托![]() 圆的方程,对称性,勾股定理
圆的方程,对称性,勾股定理
错解分析![]() 题中没有注意到圆的对称只是改变圆的位置,圆的大小并不改变,不能选取特殊点来进行解题。
题中没有注意到圆的对称只是改变圆的位置,圆的大小并不改变,不能选取特殊点来进行解题。
技巧与方法![]() 先选准圆的方程的形式,利用数形结合,并能选特殊点进行对称
先选准圆的方程的形式,利用数形结合,并能选特殊点进行对称
解![]() :(1)法一:从数的角度
:(1)法一:从数的角度
若选用标准式:设圆心P(x,y),则由|PA|=|PB|得:(x0-5)2+(y0-2)2=(x0-3)2+(y0-2)2 又2x0-y0-3=0
两方程联立得: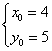 ,|PA|=
,|PA|=![]() ∴ 圆标准方程为(x-4)2+(y-5)2=10
∴ 圆标准方程为(x-4)2+(y-5)2=10
若选用一般式:设圆方程x2+y2+Dx+Ey+F=0,则圆心(![]() )
)
∴ 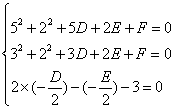 解之得:
解之得: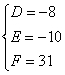
法二:从形的角度
AB为圆的弦,由平几知识知,圆心P应在AB中垂线x=4上,则由![]() 得圆心P(4,5)
得圆心P(4,5)
∴ 半径r=|PA|=![]() 显然,充分利用平几知识明显降低了计算量
显然,充分利用平几知识明显降低了计算量
(2) 设A关于直线x+2y=0的对称点为A’
由已知AA’为圆的弦 ∴ AA’对称轴x+2y=0过圆心
设圆心P(-2a,a),半径为R ,则R=|PA|=(-2a-2)2+(a-3)2
又弦长![]() ,
,![]() ∴
∴ ![]()
∴ 4(a+1)2+(a-3)2=2+![]() ∴ a=-7或a=-3
∴ a=-7或a=-3
当a=-7时,R=![]() ;当a=-3时,R=
;当a=-3时,R=![]() ∴ 所求圆方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244
∴ 所求圆方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244

练习册系列答案
相关题目