题目内容
(本题满分15分)已知 、
、 两点的坐标分别为A
两点的坐标分别为A B
B
其中 。 (1)求
。 (1)求 的表达式;(2)若
的表达式;(2)若 (
( 为坐标原点),求
为坐标原点),求 的值;
的值;
(3)若 (
( ),求函数
),求函数 的最小值。
的最小值。
 、
、 两点的坐标分别为A
两点的坐标分别为A B
B
其中
 。 (1)求
。 (1)求 的表达式;(2)若
的表达式;(2)若 (
( 为坐标原点),求
为坐标原点),求 的值;
的值;(3)若
 (
( ),求函数
),求函数 的最小值。
的最小值。(1)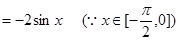 ;(2)
;(2)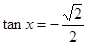 ;(3)当
;(3)当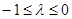 时,
时, 的最小值为
的最小值为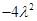 ,此时
,此时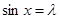 ;当
;当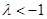 时,
时, 的最小值为
的最小值为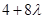 ,此时
,此时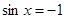 ;
;
当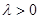 时,
时, 的最小值为0,此时
的最小值为0,此时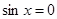
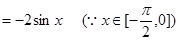 ;(2)
;(2)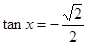 ;(3)当
;(3)当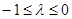 时,
时, 的最小值为
的最小值为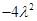 ,此时
,此时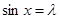 ;当
;当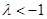 时,
时, 的最小值为
的最小值为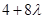 ,此时
,此时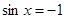 ;
;当
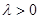 时,
时, 的最小值为0,此时
的最小值为0,此时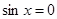
本试题主要是考查了向量的数量积公式的运用,以向量的数量积性质的运用,和三角函数的性质的综合运用。
(1)利用向量的平方就是向量的模的平方可以得到解答
(2)因为 ,然后将利用二倍角公式化为单角的三角函数关系式,分子和分母分别除以该角的余弦值的平方,得到结论。
,然后将利用二倍角公式化为单角的三角函数关系式,分子和分母分别除以该角的余弦值的平方,得到结论。
(3)运用向量的模的定义和向量的数量积的性质可知表示出y=f(x),然后后借助于角的范围求解最值。
解:(1)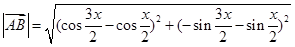
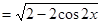
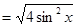
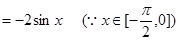
(2)∵ , ∴
, ∴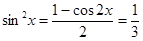 ,
,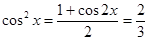
又 , ∴
, ∴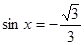 ,
,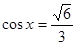 .∴
.∴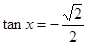 。
。
(3) =
= =
=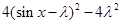
∵ ,∴
,∴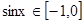
∴当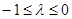 时,
时, 的最小值为
的最小值为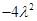 ,此时
,此时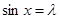 ;
;
当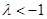 时,
时, 的最小值为
的最小值为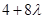 ,此时
,此时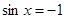 ;
;
当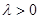 时,
时, 的最小值为0,此时
的最小值为0,此时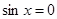
(1)利用向量的平方就是向量的模的平方可以得到解答
(2)因为
 ,然后将利用二倍角公式化为单角的三角函数关系式,分子和分母分别除以该角的余弦值的平方,得到结论。
,然后将利用二倍角公式化为单角的三角函数关系式,分子和分母分别除以该角的余弦值的平方,得到结论。(3)运用向量的模的定义和向量的数量积的性质可知表示出y=f(x),然后后借助于角的范围求解最值。
解:(1)
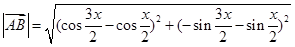
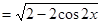
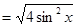
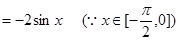
(2)∵
 , ∴
, ∴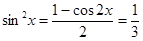 ,
,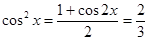
又
 , ∴
, ∴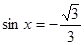 ,
,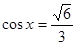 .∴
.∴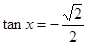 。
。(3)
 =
= =
=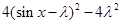
∵
 ,∴
,∴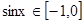
∴当
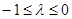 时,
时, 的最小值为
的最小值为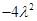 ,此时
,此时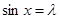 ;
;当
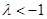 时,
时, 的最小值为
的最小值为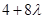 ,此时
,此时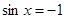 ;
;当
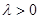 时,
时, 的最小值为0,此时
的最小值为0,此时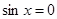

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 ,
, ,则
,则 的最小值是
的最小值是



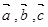 ,其中
,其中 ,
, ,且
,且 ∥
∥ ,求
,求 ,且
,且 ,求
,求 夹角的余弦值.
夹角的余弦值.
 ,
,
 ,且
,且 ,则
,则 的值为( )
的值为( )



 ,
, ,则
,则 在
在 上的投影为( ▲ )
上的投影为( ▲ )



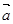 |=|
|=|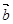 |=|
|=|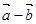 |=2,则|
|=2,则|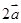
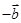 |的值为
|的值为  ,
, 且
且 ∥
∥ ,则
,则 ( )
( )

 ,它们的夹角为
,它们的夹角为  ( )
( )


