题目内容
在 中,角
中,角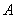 、
、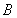 、
、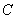 所对应的边为
所对应的边为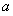 、
、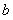 、
、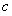 .
.
(1)若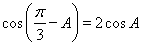 ,求
,求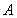 的值;
的值;
(2)若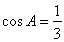 ,且
,且 的面积
的面积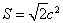 ,求
,求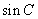 的值.
的值.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)在等式 中利用差角公式化简求出
中利用差角公式化简求出 的值,从而求出角
的值,从而求出角 的值;(2)解法1是先求出
的值;(2)解法1是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,最后利用正弦定理求出
的等量关系,最后利用正弦定理求出 的值;解法2是是先求出
的值;解法2是是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,通过观察三者之间的等量关系发现
的等量关系,通过观察三者之间的等量关系发现 、
、 、
、 三者满足勾股定理,最后在直角三角形中求出
三者满足勾股定理,最后在直角三角形中求出 的值;解法3是先求出
的值;解法3是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,最后利用三角形的面积公式求出
的等量关系,最后利用三角形的面积公式求出 的值;解法4是先求出
的值;解法4是先求出 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,从而得出
之间的等量关系,从而得出 与
与 的等量关系,并利用
的等量关系,并利用 得出
得出 和
和 的值,最后利用
的值,最后利用 求出
求出 的值.
的值.
试题解析:(1)由 ,得
,得 ,
,
 ,
, ,
, ,
,
 ,
, ;
;
(2)解法1: ,
, ,
, ,
,
由 ,得
,得 ,
,
由余弦定理得: ,
, ,
,
由正弦定理得: ,即
,即 ,
, .
.
解法2: ,
, ,
, ,
,
由 得
得 ,
,
由余弦定理得: ,
, ,
,
 ,
, 是直角三角形,角
是直角三角形,角 为直角,
为直角, ;
;
解法3: ,
, ,
, ,
,
由 得
得
由余弦定理得: ,
, ,
,
又 ,得
,得 ,
, ;
;
解法4: ,
, ,
, ,
,
由 得
得 ,
,
由正弦定理得: ,则
,则 ,
,
 ,
, ,
,
整理得 ,代入
,代入 ,得
,得 ,
,
由 知
知 ,
, .
.
考点:1.两角差的余弦公式;2.正弦定理;3.余弦定理;4.三角形的面积公式

练习册系列答案
相关题目
 中,角
中,角 、
、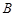 、
、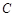 所对应的边分别为
所对应的边分别为 、
、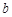 、
、 ,且满足
,且满足 .
. ,求
,求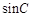 的值.
的值. 中,角
中,角 、
、 、
、 所对应的边分别为
所对应的边分别为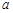 、
、 、
、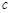 ,若
,若 ,角
,角 成等差数列,则角
成等差数列,则角 中,角
中,角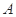 、
、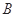 、
、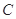 所对应的边分别为
所对应的边分别为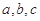 ,
,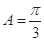 ,
,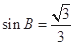
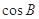 的值;
的值;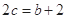 ,求边长
,求边长
 中,角
中,角 、
、 、
、 所对应的边分别为
所对应的边分别为 、
、 、
、 ,且满足
,且满足
 ,求实数
,求实数 的值。
的值。 ,求
,求 的值.
的值.