题目内容
已知函数
，
R．
（1）求
的最小值，并求出相应的
值的集合；
（2）求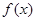
的单调递减区间．
，R．（1）求
的最小值，并求出相应的值的集合；（2）求
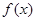的单调递减区间．最小值为
,相应的的取值的集合为
.
（2）函数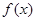的单调递减区间为
．
,相应的的取值的集合为.（2）函数
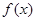的单调递减区间为．试题分析：（1）利用和差倍半的三角函数公式，化简得到
，进一步求的最小值，并求出相应的值的集合.（2）利用复合函数的单调性，解不等式
得
，求得函数的单调减区间.本题较为简单，关键是要正确应用公式，将函数加以化简.
试题解析：（1）
.（6分）所以函数
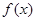的最小值为,此时
满足
,即相应的
的取值的集合为.（9分）（2）由
得所以函数
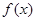的单调递减区间为．（12分）
练习册系列答案
相关题目
.
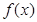的最小正周期；
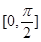上的最小值和最大值.
x+
)(
<
的值分别是（ ）
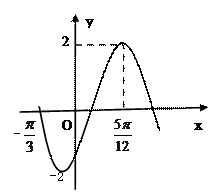
和x=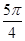
是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴，则φ=( )
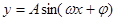在一个周期内的图象如右，此函数的解析式为（ ）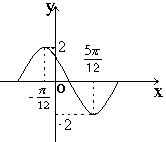
，
)图像的一部分．为了得到这个函数的图像，只要将y＝sin x(x∈R)的图像上所有的点( )
.向左平移
个单位长度，再把所得各点的横坐标缩短到原来的
，纵坐标不变.
.向左平移
.向左平移
个单位长度，再把所得各点的横坐标缩短到原来的
.向左平移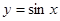
关于直线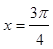
对称的曲线是（ ）
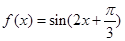，则下列结论正确的是
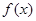的图像关于直线
对称
对称
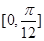上为增函数
的最大值为
，最小正周期为
，则有序数对
为 .