题目内容
（2011•浙江）设a，b，c为实数，f（x）=（x+a）（x2+bx+c），g（x）=（ax+1）（cx2+bx+1）．记集合S={x|f（x）=0，x∈R}，T={x|g（x）=0，x∈R}．若{S}，{T}分别为集合S，T 的元素个数，则下列结论不可能的是（ ）
| A．{S}=1且{T}=0 | B．{S}=1且{T}=1 | C．{S}=2且{T}=2 | D．{S}=2且{T}=3 |
D
解析
练习册系列答案
相关题目
设全集U=R，A={x|x(x-2)<0}，B={x|y=ln(1-x)<0}，则图中阴影部分表示的集合为( )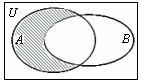
| A．{x|0<x≤1} | B．{x|1≤x<2} |
| C．{x|x≥1} | D．{x|x≤1} |
设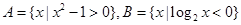
,则
( )
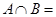A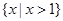． | B． | C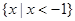． | D． |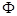
设集合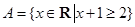
，集合
，则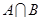
=( )
A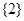． | B． |
C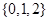． | D． |
设全集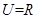
，
，
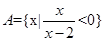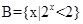，则图中阴影部分表示的集合为（ ）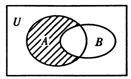
A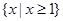． | B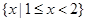． | C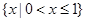． | D． |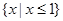
已知集合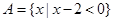
，
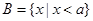，若
，则实数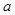
的取值范围是（ ）
A． | B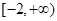． | C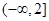． | D． |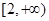
设集合A＝{1,4，x}，B＝{1，x2}且A∪B＝{1,4，x}，则满足条件的实数x的个数是( )
| A．1个 | B．2个 | C．3个 | D．4个 |
已知全集U＝R，集合P＝{x|x2≤1}，那么∁UP＝( )
| A．(－∞，－1) | B．(1，＋∞) |
| C．(－1,1) | D．(－∞，－1)∪(1，＋∞) |
设集合M={x|x2+2x=0，x∈R}，N={x|x2﹣2x=0，x∈R}，则M∪N=（ ）
| A．{0} | B．{0，2} | C．{﹣2，0} | D．{﹣2，0，2} |