Question

已知a，b，a+b成等差数列，a，b，ab成等比数列，则椭圆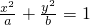，则椭圆的离心率是________．

Answer 1

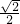
分析：利用a，b，a+b成等差数列，a，b，ab成等比数列可求得a，b，从而可求得椭圆的离心率．
解答：∵a，b，a+b成等差数列，
∴2b=a+a+b，
∴b=2a；①
又a，b，ab成等比数列，故b≠0，a≠0；
∴b²=a•ab，
∴b=a²；②
由①②得：a=2，b=4．
∵椭圆的方程为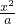+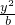=1，
∴椭圆的方程为+=1，其长半轴为2．
∴c==，
∴椭圆的离心率e==．
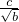故答案为：．
点评：本题考查椭圆的简单性质，着重考查等差数列与等比数列的通项公式，考查运算能力，属于中档题．