题目内容
 为了加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取了50名学生的成绩进行统计.请你根据尚未完成的频率分布表,解答下列问题:
为了加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取了50名学生的成绩进行统计.请你根据尚未完成的频率分布表,解答下列问题:| 分组 | 频数 | 频率 | |
| 第1组 | 60.5-70.5 | 0.26 | |
| 第2组 | 70.5-80.5 | 15 | |
| 第3组 | 80.5-90.5 | 18 | 0.36 |
| 第4组 | 90.5-100.5 | ||
| 合计 | 50 | 1 | |
(2)若成绩在95.5分以上的学生为一等奖,试估计全校获一等奖的人数,现在从全校所有一等奖的同学中随机抽取2名同学代表学校参加决赛,某班共有2名同学荣获一等奖,求该班同学参加决赛的人数恰为1人的概率.
分析:(1)根据频数=样本容量×频率,频率=
可求出频率分布表中空格的数据,然后根据频率分布表作出频率分布直方图即可;
(2)求出成绩在95.5分以上的学生数,从中选取2人有
=66种选法,其中某班恰有1人的选法有
×
=20种选法,根据古典概型概率计算公式求解.
| 频数 |
| 样本容量 |
(2)求出成绩在95.5分以上的学生数,从中选取2人有
| C | 2 12 |
| C | 1 2 |
| C | 1 10 |
解答:解:(1)第1组的频数为0.26×50=13;第2组的频率为
=03;第4组的频数为50-18-15-13=4,频率为
=0.08,其频率分布表如表:
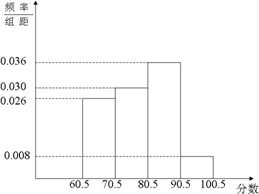
根据频率分布表作出频率分布直方图如图:
(2)成绩在95.5分以上的学生数为150×0.08=12人,
从中选取2人有
=66种选法;
其中某班恰有1人的选法有
×
=20种选法,
∴该班同学参加决赛的人数恰为1人的概率为
=
.
| 15 |
| 50 |
| 4 |
| 50 |
| 分组 | 频数 | 频率 | |
| 第1组 | 60.5-70.5 | 13 | 0.26 |
| 第2组 | 70.5-80.5 | 15 | 0.30 |
| 第3组 | 80.5-90.5 | 18 | 0.36 |
| 第4组 | 90.5-100.5 | 4 | 0.08 |
| 合计 | 50 | 1 | |

(2)成绩在95.5分以上的学生数为150×0.08=12人,
从中选取2人有
| C | 2 12 |
其中某班恰有1人的选法有
| C | 1 2 |
| C | 1 10 |
∴该班同学参加决赛的人数恰为1人的概率为
| 20 |
| 66 |
| 10 |
| 33 |
点评:本题考查了频率分布表与频率分布直方图,考查了古典概型的概率计算,考查了学生的运算能力与作图能力.

练习册系列答案
相关题目