题目内容
若实数x，y满足不等式组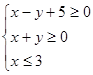
则2x＋4y的最小值是
| A．6 | B．4 | C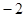． | D． |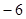
D
解析试题分析：因为实数x，y满足不等式组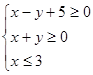对应的平面区域如下图示：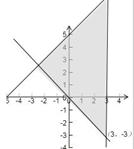
当直线z=2x+4y过（3，-3）时，Z取得最小值-6．故答案为D
考点：线性规划问题
点评：用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解
练习册系列答案
阅读快车系列答案
相关题目
设不等式组 
所表示的平面区域是
，平面区域
与关于直线
对称.对于中的任意一点
与中的任意一点
,
的最小值等于( )
A． | B．4 | C． | D．2 |
如果实数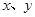
满足条件
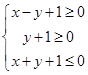，那么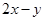
的最大值为（ ）
A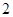． | B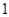． | C． | D． |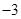
设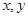
满足约束条件
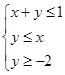,则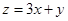
的最大值为 （ ）
| A．5 | B．3 | C．7 | D．-8 |
已知实数x,y满足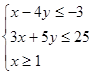
,若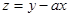
取得最大值时的最优解
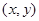有无数个,则a的值为（ ）
| A．0 | B．2 | C．-1 | D． |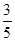
设平面区域D是由双曲线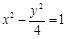
的两条渐近线和直线
所围成三角形的边界及内部．当
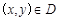时，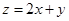
的最大值为（ ）.
| A．12 | B．10 | C．8 | D．6 |
如图，阴影部分（含边界）所表示的平面区域对应的约束条件是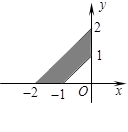
A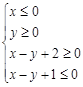． | B． |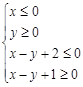
C． | D． |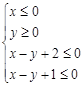
设实数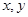
满足约束条件：
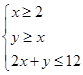，则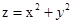
的最大值为（ ）。
A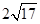． | B．68 | C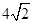． | D．32 |
若实数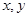
满足
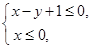则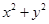
的最小值是（ ）
A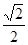． | B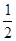． | C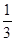． | D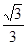． |