题目内容
已知______________________________.(先在横线上填上一个结论,然后再解答)
构建问题:已知![]() ≤a≤1,若f(x)=ax2-2x+1在[1,3]上的最大值为M(a),最小值为N(a),设g(a)=M(a)-N(a).
≤a≤1,若f(x)=ax2-2x+1在[1,3]上的最大值为M(a),最小值为N(a),设g(a)=M(a)-N(a).
判断函数g(a)的单调性,并求出g(a)的最小值.
解析:∵f(x)=a(x-![]() )2+1-
)2+1-![]() ,
,
∴f(x)的图象为开口向上的抛物线.
∵1≤![]() ≤3,x∈[1,3],
≤3,x∈[1,3],
当x=![]() 时,f(x)有最小值N(a)=1-
时,f(x)有最小值N(a)=1-![]() ,f(1)=a-1,f(3)=9a-5,f(1)-f(3)=-8(a-
,f(1)=a-1,f(3)=9a-5,f(1)-f(3)=-8(a-![]() ).
).
当![]() <a≤1时,f(1)<f(3),
<a≤1时,f(1)<f(3),
∴M(a)=9a-5.
当![]() ≤a≤
≤a≤![]() 时,f(1)≥f(3),
时,f(1)≥f(3),
∴M(a)=a-1.
∴g(a)=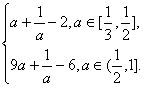
设![]() ≤a1≤a2≤
≤a1≤a2≤![]() ,则g(a1)-g(a2)=(a1-a2)(1-
,则g(a1)-g(a2)=(a1-a2)(1-![]() )>0,
)>0,
∴g(a1)>g(a2).
∴g(a)在[![]() ,
,![]() ]上是减函数.
]上是减函数.
同理,可证g(a)在(![]() ,1]上是增函数.
,1]上是增函数.
∴当a=![]() 时,g(a)有最小值
时,g(a)有最小值![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
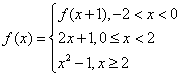 ,
,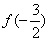 的值.
的值.