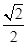Question

设两条直线的方程分别为x+y+a=0，x+y+b=0，已知a，b是方程x²+x+c=0的两个实根，且0≤c≤

1

8

，则这两条直线之间的距离的最大值和最小值分别是

 

．

Answer 1

分析：利用方程的根，求出a，b，c的关系，求出平行线之间的距离表达式，然后求解距离的最值．

解答：解：因为a，b是方程x²+x+c=0的两个实根，
所以a+b=-1，ab=c，两条直线之间的距离d=

|a-b|

2

，
∴d²=

(a+b)2-4ab

2

=

1-4c

2

，因为0≤c≤

1

8

，
所以

1

2

≤1-4c≤1，
即d²∈[

1

4

，

1

2

]，所以两条直线之间的距离的最大值和最小值分别是

2

2

，

1

2

．
故答案为：

2

2

，

1

2

点评：本题考查平行线之间的距离的求法，函数的最值的求法，考查计算能力．