Question

已知圆O的半径为1，PA、PB为该圆的两条切线，A、B为两切点，求

PA

•

PB

的最小值．

Answer 1

分析：设PA=PB=x（x＞0），∠APO=α，则∠APB=2α，PO=

1+x2

，sinα=

1

1+x2

，计算 

PA

•

PB

=

(x2+1)2-3(x2+1)+2

x2+1

，再利用基本不等式求得它的最小值．

解答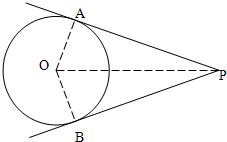：解：如图所示：设PA=PB=x（x＞0），∠APO=α，则∠APB=2α，PO=

1+x2

，sinα=

1

1+x2

，
∴

PA

•

PB

=|

PA

|•|

PB

|cos2α=x²（1-2sin²α）=

x2(x2-1)

x2+1

=

x4-x2

x2+1

 
=

(x2+1)2-3(x2+1)+2

x2+1

=（x²+1）-3+

2

x2+1

≥2

2

-3，
当且仅当x²+1=

2

x2+1

，即 x=

2 -1

时，等号成立，
故

PA

•

PB

的最小值为-3+2

2

，此时，x=

2 -1

．

点评：本题主要考查两个向量的数量的定义和两个向量数量积公式的应用，基本不等式的应用，直线和圆的位置关系，属于中档题．