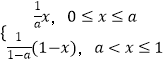题目内容
【题目】在平面直角坐标系xOy中，曲线y=x2﹣6x+1与坐标轴的交点都在圆C上．
（Ⅰ）求圆C的方程；
（Ⅱ）若圆C与直线x﹣y+a=0交与A，B两点，且OA⊥OB，求a的值．
【答案】解：（Ⅰ）法一：曲线y=x2﹣6x+1与y轴的交点为（0，1），与x轴的交点为（3+2 
，0），（3﹣2 ，0）．可知圆心在直线x=3上，故可设该圆的圆心C为（3，t），则有32+（t﹣1）2=（2 ）2+t2 ， 解得t=1，故圆C的半径为 
，所以圆C的方程为（x﹣3）2+（y﹣1）2=9． 法二：圆x2+y2+Dx+Ey+F=0
x=0，y=1有1+E+F=0
y=0，x2 ﹣6x+1=0与x2+Dx+F=0是同一方程，故有D=﹣6，F=1，E=﹣2，
即圆方程为x2+y2﹣6x﹣2y+1=0
（Ⅱ）设A（x1 ， y1），B（x2 ， y2），其坐标满足方程组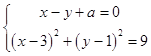
，消去y，得到方程2x2+（2a﹣8）x+a2﹣2a+1=0，由已知可得判别式△=56﹣16a﹣4a2＞0．
在此条件下利用根与系数的关系得到x1+x2=4﹣a，x1x2= 
①，
由于OA⊥OB可得x1x2+y1y2=0，又y1=x1+a，y2=x2+a，所以可得2x1x2+a（x1+x2）+a2=0②
由①②可得a=﹣1，满足△=56﹣16a﹣4a2＞0．故a=﹣1
【解析】（Ⅰ）法一：写出曲线与坐标轴的交点坐标，利用圆心的几何特征设出圆心坐标，构造关于圆心坐标的方程，通过解方程确定出圆心坐标，进而算出半径，写出圆的方程； 法二：可设出圆的一般式方程，利用曲线与方程的对应关系，根据同一性直接求出参数，（Ⅱ）利用设而不求思想设出圆C与直线x﹣y+a=0的交点A，B坐标，通过OA⊥OB建立坐标之间的关系，结合韦达定理寻找关于a的方程，通过解方程确定出a的值．
【考点精析】认真审题，首先需要了解圆的标准方程(圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程)．
