题目内容
已知△ABC中,cos(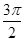 -A)+cos(π+A)=-
-A)+cos(π+A)=-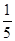 .
.
(1)判断△ABC是锐角三角形还是钝角三角形;
(2)求tanA的值.
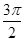 -A)+cos(π+A)=-
-A)+cos(π+A)=-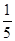 .
.(1)判断△ABC是锐角三角形还是钝角三角形;
(2)求tanA的值.
(1)△ABC是钝角三角形
(2)-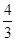
(2)-
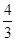
解:(1)由已知得,-sinA-cosA=-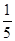 .
.
∴sinA+cosA=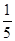 .①
.①
①式平方得,1+2sinAcosA=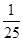 ,
,
∴sinAcosA=-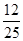 <0,
<0,
又∵0<A<π,∴sinA>0,cosA<0.
∴A为钝角,故△ABC是钝角三角形.
(2)∵(sinA-cosA)2=1-2sinAcosA=1+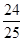 =
=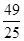 .
.
又∵sinA>0,cosA<0,
∴sinA-cosA>0,
∴sinA-cosA=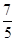 ,
,
又由已知得sinA+cosA=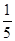 ,
,
故sinA=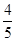 ,cosA=-
,cosA=-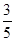 ,
,
∴tanA=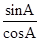 =-
=-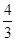 .
.
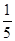 .
.∴sinA+cosA=
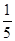 .①
.①①式平方得,1+2sinAcosA=
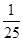 ,
,∴sinAcosA=-
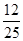 <0,
<0,又∵0<A<π,∴sinA>0,cosA<0.
∴A为钝角,故△ABC是钝角三角形.
(2)∵(sinA-cosA)2=1-2sinAcosA=1+
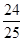 =
=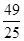 .
.又∵sinA>0,cosA<0,
∴sinA-cosA>0,
∴sinA-cosA=
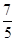 ,
,又由已知得sinA+cosA=
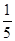 ,
,故sinA=
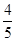 ,cosA=-
,cosA=-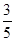 ,
,∴tanA=
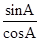 =-
=-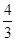 .
.
练习册系列答案
相关题目
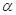 是第二象限角,且
是第二象限角,且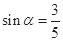 ,则
,则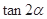 的值为( ).
的值为( ).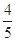
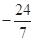
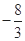
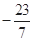
 +5=0,tan(π+α)+6sin(π+β)=1,则sin α的值是______.
+5=0,tan(π+α)+6sin(π+β)=1,则sin α的值是______.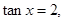 则
则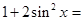 ( )
( )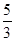
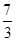
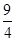
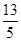
 -x)=
-x)=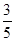 ,则cos(
,则cos(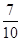 π-x)=( )
π-x)=( )
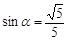 ,则
,则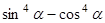 的值为( )
的值为( )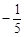
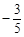
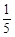
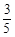
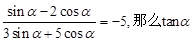 的值为( )
的值为( )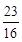
 ,则
,则 = .
= .