题目内容
如图,在游乐场,有一种游戏是向一个画满均匀方格的大桌面上投硬币,若硬币刚巧落在任何一个方格的范围内(不与方格线重叠),便可获奖.如果硬币的直径为2cm,而方格的边长为5cm,随机投掷一个硬币,获奖的概率有多大?
【答案】分析:如图所示,设正方形ABCD是边长为5cm的一个方格,可得当硬币的圆心位于正方形ABCD内部且在小正方形EFGH内部时,可使硬币刚巧落在一个方格的范围.结合题中数据,算出两个正方形的面积,利用几何概型计算公式即可算出获奖的概率.
解答: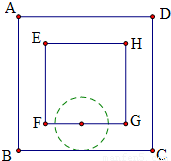 解:设正方形ABCD是边长为5cm的一个方格,如图所示
解:设正方形ABCD是边长为5cm的一个方格,如图所示
由硬币的直径为2cm,得硬币半径为1cm
设正方形EFGH在正方形ABCD内部,且互相平行的边之间的距离等于1
可得当硬币的圆心位于正方形EFGH内部时,所投的硬币与ABCD的边没有交点
∵正方形EFGH的边长为5-2=3cm,
∴正方形EFGH的面积为S=32=9cm2
结合正方形ABCD的面积S'=52=25cm2,可得随机投掷一个硬币,获奖的概率
P=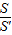 =
=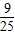 =0.36
=0.36
答:向画满均匀方格的大桌面上随机投掷一个硬币,获奖的概率为0.36.
点评:本题给出投掷硬币的事件,求获奖的概率.着重考查了圆的性质、正方形的性质和几何概型计算公式等知识,属于中档题.
解答:
 解:设正方形ABCD是边长为5cm的一个方格,如图所示
解:设正方形ABCD是边长为5cm的一个方格,如图所示由硬币的直径为2cm,得硬币半径为1cm
设正方形EFGH在正方形ABCD内部,且互相平行的边之间的距离等于1
可得当硬币的圆心位于正方形EFGH内部时,所投的硬币与ABCD的边没有交点
∵正方形EFGH的边长为5-2=3cm,
∴正方形EFGH的面积为S=32=9cm2
结合正方形ABCD的面积S'=52=25cm2,可得随机投掷一个硬币,获奖的概率
P=
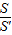 =
=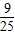 =0.36
=0.36答:向画满均匀方格的大桌面上随机投掷一个硬币,获奖的概率为0.36.
点评:本题给出投掷硬币的事件,求获奖的概率.着重考查了圆的性质、正方形的性质和几何概型计算公式等知识,属于中档题.

练习册系列答案
相关题目
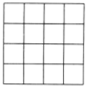 如图,在游乐场,有一种游戏是向一个画满均匀方格的大桌面上投硬币,若硬币刚巧落在任何一个方格的范围内(不与方格线重叠),便可获奖.如果硬币的直径为2cm,而方格的边长为5cm,随机投掷一个硬币,获奖的概率有多大?
如图,在游乐场,有一种游戏是向一个画满均匀方格的大桌面上投硬币,若硬币刚巧落在任何一个方格的范围内(不与方格线重叠),便可获奖.如果硬币的直径为2cm,而方格的边长为5cm,随机投掷一个硬币,获奖的概率有多大?