题目内容
(上海春卷20)已知函数f(x)=loga(8-2x)(a>0且a≠0)
(1)若函数f(x)的反函数是其本身,求a的值;
(2)当a>1时,求函数y=f(x)+f(-x)的最大值.
解:(1)∵函数f(x)=loga(8-2x),∴8-2x =af(x),x=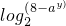 ,
,
故反函数为 y=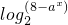 ,∴loga(8-2x)=
,∴loga(8-2x)=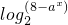 ,∴a=2.
,∴a=2.
(2)当a>1时,由题意知,8-2x>0,∴x<3,函数y=f(x)+f(-x)的定义域(-3,3),
函数y=f(x)+f(-x)=loga(8-2x)+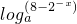 =
=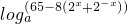 ,
,
∴2x+2-x≥2,当且仅当x=0时,取等号.∴0<65-8(2x+2-x )≤49,
当a>1时,函数y=f(x)+f(-x)在x=0处取得最大值loga49.
分析:(1)先求出反函数的解析式,利用反函数和原函数的解析式相同,求出a的值.
(2)当a>1时,先求出函数的定义域,化简函数的解析式,利用基本不等式求出最值.
点评:本题考查求函数的反函数的方法,对数式的运算性质,基本不等式的应用.
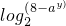 ,
,故反函数为 y=
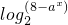 ,∴loga(8-2x)=
,∴loga(8-2x)=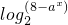 ,∴a=2.
,∴a=2.(2)当a>1时,由题意知,8-2x>0,∴x<3,函数y=f(x)+f(-x)的定义域(-3,3),
函数y=f(x)+f(-x)=loga(8-2x)+
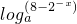 =
=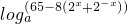 ,
,∴2x+2-x≥2,当且仅当x=0时,取等号.∴0<65-8(2x+2-x )≤49,
当a>1时,函数y=f(x)+f(-x)在x=0处取得最大值loga49.
分析:(1)先求出反函数的解析式,利用反函数和原函数的解析式相同,求出a的值.
(2)当a>1时,先求出函数的定义域,化简函数的解析式,利用基本不等式求出最值.
点评:本题考查求函数的反函数的方法,对数式的运算性质,基本不等式的应用.

练习册系列答案
相关题目