题目内容
椭圆C的中心坐标为原点O,焦点在y轴上,焦点到相应准线的距离以及离心率均为 ,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A
,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A .
.(1)求椭圆方程;
(2)若
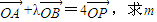 的取值范围?.
的取值范围?.
【答案】分析:(1)利用待定系数法求椭圆的方程,设出椭圆C的标准方程,依条件得出a,b的方程,求出a,b即得椭圆C的方程.
(2)先设l与椭圆C交点为A(x1,y1),B(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量条件即可求得m的取值范围,从而解决问题.
解答:解:(1)设椭圆C的方程: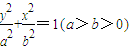 ,则c2=a2-b2,
,则c2=a2-b2,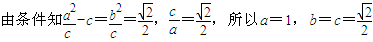 ,
,
故椭圆C的方程为y2+2x2=1.(4分)
(2)由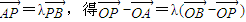 ,
,
∴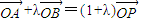 .
.
∵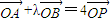 ,
,
∴λ+1=4,λ=3.
设l与椭圆C交点为A(x1,y1),B(x2,y2),
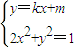
得(k2+2)x2+2kmx+(m2-1)=0,
因此△=(2km)2-4(k2+2)(m2-1)
=4(k2-2m2+2)>0,①
则x1+x2=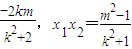 .
.
∵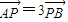 ,∴-x1=3x2,得
,∴-x1=3x2,得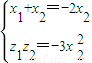
得3(x1+x2)2+4x1x2=0,
∴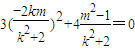 ,
,
整理得:4k2m2+2m2-k2-2=0.
当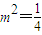 时,上式不成立.
时,上式不成立.
∴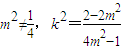 .
.
由①式得k2>2m2-2,
∵λ=3,∴k≠0,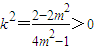 ,
,
所以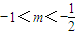 或
或 .
.
即所求m的取值范围为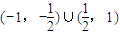 (14分)
(14分)
点评:本题考查用待定系数法求曲线方程的方法,设计新颖,基础性强 待定系数法求曲线方程,如何处理直线与圆锥曲线问题,向量问题,成为解决本题的关键.
(2)先设l与椭圆C交点为A(x1,y1),B(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量条件即可求得m的取值范围,从而解决问题.
解答:解:(1)设椭圆C的方程:
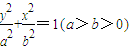 ,则c2=a2-b2,
,则c2=a2-b2,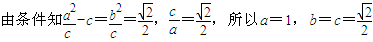 ,
,故椭圆C的方程为y2+2x2=1.(4分)
(2)由
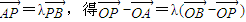 ,
,∴
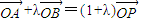 .
.∵
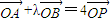 ,
,∴λ+1=4,λ=3.
设l与椭圆C交点为A(x1,y1),B(x2,y2),
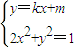
得(k2+2)x2+2kmx+(m2-1)=0,
因此△=(2km)2-4(k2+2)(m2-1)
=4(k2-2m2+2)>0,①
则x1+x2=
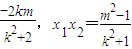 .
.∵
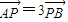 ,∴-x1=3x2,得
,∴-x1=3x2,得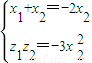
得3(x1+x2)2+4x1x2=0,
∴
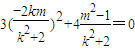 ,
,整理得:4k2m2+2m2-k2-2=0.
当
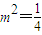 时,上式不成立.
时,上式不成立.∴
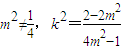 .
.由①式得k2>2m2-2,
∵λ=3,∴k≠0,
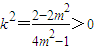 ,
,所以
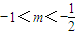 或
或 .
.即所求m的取值范围为
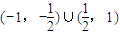 (14分)
(14分)点评:本题考查用待定系数法求曲线方程的方法,设计新颖,基础性强 待定系数法求曲线方程,如何处理直线与圆锥曲线问题,向量问题,成为解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A
,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A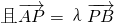 .
.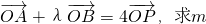 的取值范围?.
的取值范围?.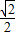 ,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A
,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A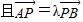 .
.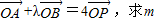 的取值范围?.
的取值范围?. ,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A
,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A .
. 的取值范围?.
的取值范围?.