题目内容
下列四组函数是同一函数的个数为（ ）
（1）y1=
，y2=x-5；
（2）y1=
•
，y2=
（3）f（x）=x，g(x)=
；
（4）f1(x)=(
)2，f2（x）=2x-5．
（1）y1=
| (x+3)(x-5) |
| x+3 |
（2）y1=
| x+1 |
| x-1 |
| (x+1)(x-1) |
（3）f（x）=x，g(x)=
| x2 |
（4）f1(x)=(
| 2x-5 |
分析：当两个函数表示同一个函数时，要求函数的三要素（定义域、值域、对应法则）都相同，分别判断四个答案中函数的定义域和解析式是否一致即可得到答案．
解答：解：（1）中，y1=
，y2=x-5的定义域不相同，解析式不相同，故表示不同函数；
（2）中，f（x）=
•
的定义域是{x|x=1}，g（x）=
的定义域是{x|-1＜x＜1}，两个函数的定义域不同，故不表示同一函数；
（3）中，f（x）=x，g（x）=
的定义域不同，故不表示同一函数；
（4）中，f1(x)=(
)2，f2（x）=2x-5定义域，解析式不相同，故不表示同一函数；
故选A．
| (x+3)(x-5) |
| x+3 |
（2）中，f（x）=
| x+1 |
| x-1 |
| (x+1)(x-1) |
（3）中，f（x）=x，g（x）=
| x2 |
（4）中，f1(x)=(
| 2x-5 |
故选A．
点评：本题考查两函数表示同一个函数的条件，当两个函数表示同一个函数时，要求函数的三要素（定义域、值域、对应法则）都相同．要求会求函数的定义域和值域，并会化简函数解析式．属简单题．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
下列四组函数中，两函数是同一函数的是（ ）
A、f（x）=
| |||||
B、f（x）=(
| |||||
C、f（x）=x与f（x）=
| |||||
D、f(x)=
|
＝1与lg(y＋1)＝lg(x－2)
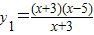，y2=x-5； 
，
； 
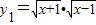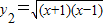
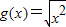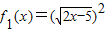，f2（x）=2x-5．
，
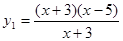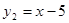； (2) 
，
，
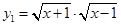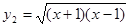
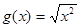； （4）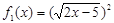
，