Question

如果a，b是异面直线，P是不在a，b上的任意一点，下列四个结论：
①过点P一定可以作直线L与a，b都相交；
②过点P一定可以作直线L与a，b都垂直；
③过点P一定可以作平面α与a，b都平行；
④过点P一定可以作直线L与a，b都平行；
上述结论中正确的是

②

．

Answer 1

分析：以正方体为实例，举出反例P=C₁时，可判断①③错误；根据平行公理可判断④错误．

解答：解：如图所示：

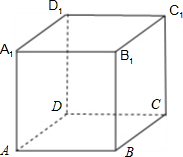
A₁D₁与CD异面，P=C₁时，不满足条件①
A₁D₁与CD异面，而DD₁与它们都垂直，过P作DD₁的平行线，满足条件②
A₁D₁与CD异面，P=C₁时，不满足条件③
若存在一条直线与它们都平行，由平行公理可得A₁D₁∥CD，这与A₁D₁与CD异面相矛盾，故条件④错误；
故答案为：②

点评：本题以命题的真假判断为载体考查了空间线面关系，熟练掌握空间线面关系的定义及几何特征是解答的关键．