题目内容
若(x2－
)n的展开式中含x的项为第6项，设(1－3x)n＝a0＋a1x＋a2x2＋…＋anxn，则a1＋a2＋…＋an的值为________．
)n的展开式中含x的项为第6项，设(1－3x)n＝a0＋a1x＋a2x2＋…＋anxn，则a1＋a2＋…＋an的值为________．255
本题主要考查二项式定理、特殊赋值法等知识，考查方程思想．
二项式(x2－)n展开式的第6项是T5＋1＝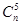
(－1)5x2n－15，令2n－15＝1得n＝8.在二项式(1－3x)8的展开式中，令x＝0得a0＝1，令x＝1得a0＋a1＋…＋a8＝28＝256，所以a1＋a2＋…＋a8＝255.
二项式(x2－
)n展开式的第6项是T5＋1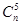＝ (－1)5x2n－15，令2n－15＝1得n＝8.在二项式(1－3x)8的展开式中，令x＝0得a0＝1，令x＝1得a0＋a1＋…＋a8＝28＝256，所以a1＋a2＋…＋a8＝255.
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
的二项展开式中，x的系数为 ．
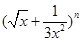的第五项的二项式系数与第三项的二项式系数的比是
，
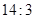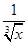)n的展开式中各项系数之和为729，则该展开式中x2的系数为________．
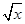)8展开式中不含x4项的系数的和为( )
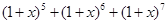的展开式中，含
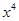的项的系数是___
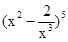展开式中的常数项为 ．（用数字作答）
，若
，
（ ）