题目内容
考查下列四个命题:
①已知直线l,二次函数的图象(抛物线)C,则“直线l与抛物线C有且只有一个公共点”是“直线l与抛物线C相切”的必要不充分条件
②“a+b=0”是“直线y=x+2与圆(x-a)2+(y+b)2=2相切”的充分不必要条件
③“a2+b2=0”是“函数f(x)=x|x+a|+b是奇函数”的充分不必要条件
④“f(x)的最小正周期为6”是“函数f(x)对于任意实数X,有f(x+3)=-
”的充分必要条件
其中所有正确的命题是( )
①已知直线l,二次函数的图象(抛物线)C,则“直线l与抛物线C有且只有一个公共点”是“直线l与抛物线C相切”的必要不充分条件
②“a+b=0”是“直线y=x+2与圆(x-a)2+(y+b)2=2相切”的充分不必要条件
③“a2+b2=0”是“函数f(x)=x|x+a|+b是奇函数”的充分不必要条件
④“f(x)的最小正周期为6”是“函数f(x)对于任意实数X,有f(x+3)=-
| 1 |
| f(x) |
其中所有正确的命题是( )
| A、①② | B、①③ | C、③④ | D、①②④ |
分析:“直线l与抛物线C有且只有一个公共点”?“直线l与抛物线C相切或相交”,“直线l与抛物线C相切”?“直线l与抛物线C有且只有一个公共点”.①成立;“a+b=0”?“直线y=x+2与圆(x-a)2+(y+b)2=2相切”,“直线y=x+2与圆(x-a)2+(y+b)2=2相切”?“a+b=0,或a+b=-4”.②成立;“a2+b2=0”?“函数f(x)=x|x+a|+b是奇函数”,③不成立;“f(x)的最小正周期为6”?“函数f(x)对于任意实数X,有f(x+3)=-
”,④不成立.
| 1 |
| f(x) |
解答:解:若“直线l与抛物线C有且只有一个公共点”,
则“直线l与抛物线C相切或相交”;
若“直线l与抛物线C相切”,
则“直线l与抛物线C有且只有一个公共点”.
故①成立;
若“a+b=0”,则“直线y=x+2与圆(x-a)2+(y+b)2=2相切”;
若“直线y=x+2与圆(x-a)2+(y+b)2=2相切”,
则“a+b=0,或a+b=-4”.
故②成立;
若“a2+b2=0”,则“函数f(x)=x|x+a|+b是奇函数”,
若“函数f(x)=x|x+a|+b是奇函数”,则“a2+b2=0”.
故③不成立;
若“f(x)的最小正周期为6”,则“函数f(x)对于任意实数X,有f(x+3)=-
”,
若“函数f(x)对于任意实数X,有f(x+3)=-
”,则“f(x)的最小正周期为6”.
故④不成立.
故选A.
则“直线l与抛物线C相切或相交”;
若“直线l与抛物线C相切”,
则“直线l与抛物线C有且只有一个公共点”.
故①成立;
若“a+b=0”,则“直线y=x+2与圆(x-a)2+(y+b)2=2相切”;
若“直线y=x+2与圆(x-a)2+(y+b)2=2相切”,
则“a+b=0,或a+b=-4”.
故②成立;
若“a2+b2=0”,则“函数f(x)=x|x+a|+b是奇函数”,
若“函数f(x)=x|x+a|+b是奇函数”,则“a2+b2=0”.
故③不成立;
若“f(x)的最小正周期为6”,则“函数f(x)对于任意实数X,有f(x+3)=-
| 1 |
| f(x) |
若“函数f(x)对于任意实数X,有f(x+3)=-
| 1 |
| f(x) |
故④不成立.
故选A.
点评:本题考查充分条件、必要条件、充要条件的性质和应用,解题时要认真审题,注意直线和曲线相切、函数的周斯等性质的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 ”的充分必要条件
”的充分必要条件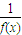 ”的充分必要条件
”的充分必要条件