题目内容
若实数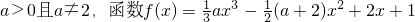 .
.
(1)若a>2,求函数f(x)的单调区间;
(2)若在区间(0,+∞)上存在一点x0,使得f(x0)<1成立,求实数a的取值范围.
解:(1)∵f(x)=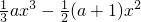 +2x+1
+2x+1
∴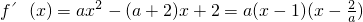 …(2分)a>2时,列表如下,
…(2分)a>2时,列表如下,
| x | 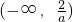 |  | 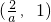 | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
∴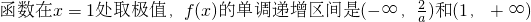
单调递减区间是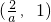
当0<a<2时,列表如下,
| x | (-∞,1) | 1 | 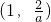 |  | 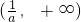 |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
∴
单调递减区间是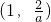
(2)因为f(0)=1,由(1)知要使在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,只需在区间(0,+∞)上f(x)极小值<1即可.
当a>2时,f(x)极小值=f(1)=2- <1,所以a>6.
<1,所以a>6.
当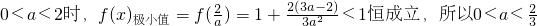 .
.
综上所述,实数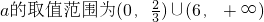
分析:(1)求出函数的导数,通过a>2,列出导函数的值的符号,确定函数f(x)的单调区间;
(2)通过f(0)=1,利用(1)要使在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,只需在区间(0,+∞)上f(x)极小值<1,即可求实数a的取值范围.
点评:本题是中档题,考查函数的导数,函数的单调性的应用,考查转化思想计算能力,同时注意分类讨论思想.近几年高考必考内容.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 .
.