题目内容
若点P(a,b)在圆C:x2+y2=1的外部,则直线ax+by+1=0与圆C的位置关系是( )A.相切
B.相离
C.相交
D.相交或相切
【答案】分析:由P在圆C外部,将得到P与圆心间的距离大于半径1,利用点到直线的距离公式表示出圆心C到直线ax+by+1=0的距离d,判断出d与r的大小关系,即可得出直线与圆的位置关系.
解答:解:∵点P(a,b)在圆C:x2+y2=1的外部,
∴a2+b2>1,
∵圆心C坐标为(0,0),半径r=1,
∴圆心到直线ax+by+1=0的距离d=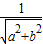 <1=r,
<1=r,
则直线ax+by+1=0与圆C的位置关系为相交.
故选C
点评:此题考查了直线与圆的位置关系,涉及的知识有:点与圆的位置关系,两点间的距离公式,以及点到直线的距离公式,其中当d<r时,直线与圆相交;当d=r时,直线与圆相切;当d>r时,直线与圆相离(d为圆心到直线的距离,r为圆的半径).
解答:解:∵点P(a,b)在圆C:x2+y2=1的外部,
∴a2+b2>1,
∵圆心C坐标为(0,0),半径r=1,
∴圆心到直线ax+by+1=0的距离d=
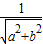 <1=r,
<1=r,则直线ax+by+1=0与圆C的位置关系为相交.
故选C
点评:此题考查了直线与圆的位置关系,涉及的知识有:点与圆的位置关系,两点间的距离公式,以及点到直线的距离公式,其中当d<r时,直线与圆相交;当d=r时,直线与圆相切;当d>r时,直线与圆相离(d为圆心到直线的距离,r为圆的半径).

练习册系列答案
相关题目