题目内容
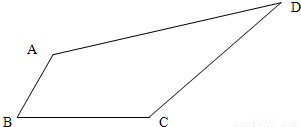
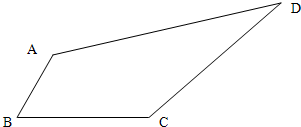如图四边形ABCD中，AB=2，BC=4，CD=3| 3 |
分析：连接AC，根据题意求出∠BAC=90°，∠ACB=30°，利用勾股定理求出AC的长，在三角形ACD中，由AC，CD及cos∠ACD的值，利用余弦定理即可求出AD的长．
解答：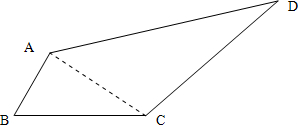
解：连接AC，则可知∠BAC=90°，∠ACB=30°，
∴根据勾股定理得：AC=2
，
在△ACD中，由余弦定理得：AD2=AC2+CD2-2AC•CD•cos∠ACD=12+27-2×2
×3
×cos120°=57，
解得：AD=
．
解：连接AC，则可知∠BAC=90°，∠ACB=30°，∴根据勾股定理得：AC=2
| 3 |
在△ACD中，由余弦定理得：AD2=AC2+CD2-2AC•CD•cos∠ACD=12+27-2×2
| 3 |
| 3 |
解得：AD=
| 57 |
点评：此题考查了余弦定理，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
如图四边形ABCD中，已知AC=
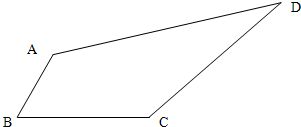如图四边形ABCD中，AB=2，BC=
,判断四边形ABCD的形状.
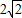，CD=7；且∠B=45°，∠C=105°，求边AD的长．