本题共有2个小题.第一个小题满分6分.第2个小题满分8分．已知数列的前项和为.且. (1)证明:是等比数列, (2)求数列的通项公式.并求出使得成立的最小正整数．题目和参考答案——青夏教育精英家教网——

题目内容

本题共有2个小题，第一个小题满分6分，第2个小题满分8分．

已知数列的前项和为，且，

（1）证明：是等比数列；

（2）求数列的通项公式，并求出使得成立的最小正整数．

【答案】

解析：(1) 当n=1时，a₁=-14；当n≥2时，a_n=S_n-S_n_-₁=-5a_n+5a_n_-₁+1，所以，

又a₁-1=-15≠0，所以数列{a_n-1}是等比数列；

(2) 由(1)知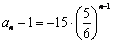：，得，

从而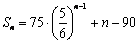(nÎN*)；

由S_n₊₁>S_n，得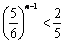，，最小正整数n=15．

练习册系列答案

华东师大版一课一练系列答案

孟建平单元测试系列答案

金考卷活页题选系列答案

上海作业系列答案

海淀名师伴你学同步学练测系列答案

非练不可系列答案

孟建平名校考卷系列答案

新课标三习五练课堂作业系列答案

金牌教练系列答案

跟我学系列答案

相关题目

本题共有2个小题，第1小题满分6分，第2小题满分10分．
已知a为实数，f(x)=a-

(x∈R)．
（1）求证：对于任意实数a，y=f（x）在（-∞，+∞）上是增函数；
（2）当f（x）是奇函数时，若方程f^-1（x）=log₂（x+t）总有实数根，求实数t的取值范围．

（2005•上海模拟）本题共有2个小题，第1小题满分8分，第2小题满分6分
过直角坐标平面xOy中的抛物线y²?2px （p＞0）的焦点F作一条倾斜角为

的直线与抛物线相交于A、B两点．
（1）用p表示A、B之间的距离并写出以AB为直径的圆C方程；
（2）若圆C于y轴交于M、N两点，写出M、N的坐标，证明∠MFN的大小是与p无关的定值，并求出这个值．

（本题满分14分）本题共有2个小题，第1小题满分8分，第2小题满分6分．

已知函数， .

（1）若，求函数的值；

（2）求函数的值域.

（本大题满分13分）本题共有2个小题，第1小题满分5分，第2小题满分8分.

如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，骨架把圆柱底面8等份，再用S平方米塑料片制成圆柱的侧面和下底面（不安装上底面）.

(1)当圆柱底面半径取何值时，取得最大值？并求出该

最大值（结果精确到0.01平方米）;

（2）在灯笼内，以矩形骨架的顶点为点，安装一些霓虹灯，当灯笼的底面半径为0.3米时，求图中两根直线与所在异面直线所成角的大小（结果用反三角函数表示）

（本小题满分12分）本题共有2个小题，第1小题满分6分，第2小题满分6分．

已知向量且与向量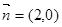夹角为，其中A，B，C是的内角。

（1）求角B的大小；

（2）求的取值范围。