题目内容
如果对于x∈R,不等式|x+1|≥kx恒成立,则k的取值范围是
[0,1]
[0,1]
.分析:由题意得要使不等式|x+1|≥kx恒成立,只要使得当x取相同的值时,y=|x+1|的图象不能在y=kx的图象的下方,画出函数y=|x+1|与y=kx的图象,如图所示:可得直线y=kx的斜率只能在0≤k≤1.
解答:解:∵不等式|x+1|≥kx恒成立,
∴y=|x+1|的图象不能在 y=kx 的图象的下方,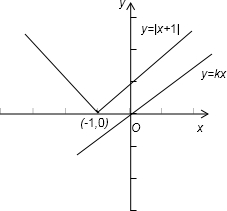
如图所示画出两个函数y=|x+1|与y=kx的图象,
根据两条直线之间的关系,得到y=kx的图象只能在与x轴重合与y=x平行之间,
∴0≤k≤1,
故答案为:[0,1]
∴y=|x+1|的图象不能在 y=kx 的图象的下方,

如图所示画出两个函数y=|x+1|与y=kx的图象,
根据两条直线之间的关系,得到y=kx的图象只能在与x轴重合与y=x平行之间,
∴0≤k≤1,
故答案为:[0,1]
点评:本题考查函数的恒成立问题,体现了数形结合的数学思想,本题解题的关键是构造新函数,在同一个坐标系中画出函数的图象,结合图象看出要求的直线的斜率的范围,本题是一个基础题.

练习册系列答案
相关题目
 成立.
成立. ,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;
,如果f(0)=1,判断g(x)=0是否有负实根并说明理由; 成立.
成立.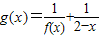 ,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;
,如果f(0)=1,判断g(x)=0是否有负实根并说明理由; 成立.
成立. ,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;
,如果f(0)=1,判断g(x)=0是否有负实根并说明理由;