题目内容
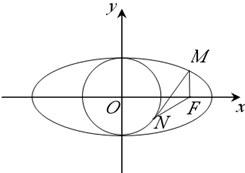
F为椭圆 的右焦点,第一象限内的点M在椭圆上,若MF⊥x轴,直线MN与圆x2+y2=1相切于第四象限内的点N,则|NF|等于( )
的右焦点,第一象限内的点M在椭圆上,若MF⊥x轴,直线MN与圆x2+y2=1相切于第四象限内的点N,则|NF|等于( )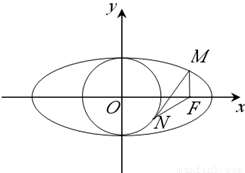
A.
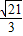
B.
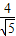
C.
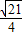
D.
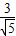
【答案】分析:根据椭圆的性质,可求出F点坐标,进而结合已知中MF⊥x轴,求出M点坐标,根据直线MN与圆相切求出点N的坐标后,代入两点之间距离公式,可得答案.
解答:解:∵F为椭圆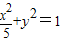 的右焦点,
的右焦点,
∴F点的坐标为(2,0)
∵MF⊥x轴,M在椭圆上且在第一象限
∴M点的坐标为(2,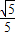 )
)
设直线MN的斜率为k(k>0)
则直线MN的方程为y-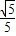 =k(x-2)
=k(x-2)
即kx-y-2k+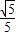 =0
=0
∵直线MN与圆x2+y2=1相切
∴原点(圆心)到直线MN的距离等于半径1,
即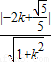 =1
=1
解得k=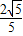 ,或k=
,或k=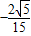 (舍去)
(舍去)
∴直线MN的方程为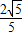 x-y-
x-y-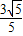 =0…①
=0…①
联立圆方程x2+y2=1可得
N点坐标为( ,
, )
)
∴|NF|=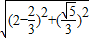 =
=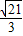
故选A
点评:本题考查的知识点是椭圆的简单性质,直线与圆的位置关系,两点之间的距离,其中求出N点坐标是解答的关键.
解答:解:∵F为椭圆
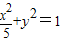 的右焦点,
的右焦点,∴F点的坐标为(2,0)
∵MF⊥x轴,M在椭圆上且在第一象限
∴M点的坐标为(2,
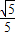 )
)设直线MN的斜率为k(k>0)
则直线MN的方程为y-
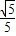 =k(x-2)
=k(x-2)即kx-y-2k+
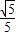 =0
=0∵直线MN与圆x2+y2=1相切
∴原点(圆心)到直线MN的距离等于半径1,
即
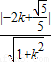 =1
=1解得k=
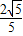 ,或k=
,或k=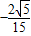 (舍去)
(舍去)∴直线MN的方程为
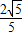 x-y-
x-y-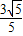 =0…①
=0…①联立圆方程x2+y2=1可得
N点坐标为(
 ,
, )
)∴|NF|=
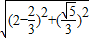 =
=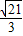
故选A
点评:本题考查的知识点是椭圆的简单性质,直线与圆的位置关系,两点之间的距离,其中求出N点坐标是解答的关键.

练习册系列答案
相关题目
 F为椭圆
F为椭圆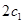 和
和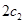 分别表示椭轨道Ⅰ和Ⅱ的焦距,用
分别表示椭轨道Ⅰ和Ⅱ的焦距,用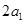 和
和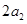
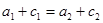 ②
②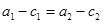 ③
③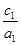 <
<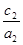 ④
④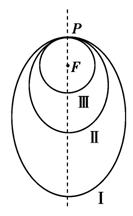
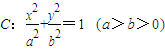 的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为
的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为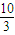 .
.