题目内容
“剪刀、石头、布”游戏的规则是:出拳之前双方齐喊口令,然后在话音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”,“剪刀”胜“布”,而“布”又胜“石头”,如果所出的拳相同,则为和局.现甲乙二人通过“剪刀、石头、布”游戏进行比赛.
(Ⅰ) 设甲乙二人每局都随机出“剪刀”、“石头”、“布”中的某一个,求甲胜乙的概率;
(Ⅱ)据专家分析,乙有以下的出拳习惯:①第一局不出“剪刀”;②连续两局的出拳方法一定不一样,即如果本局出“剪刀”,则下局将不再出“剪刀”,而是选“石头”、“布”中的某一个.假设专家的分析是正确的,甲根据专家的分析出拳,保证每一局都不输给乙.在最多5局的比赛中,谁胜的局数多,谁获胜.游戏结束的条件是:一方胜3局或赛满5局,用X表示游戏结束时的游戏局数,求X的分布列和期望.
解:(Ⅰ)根据“石头”胜“剪刀”,“剪刀”胜“布”,而“布”又胜“石头”,可得甲胜乙的概率为P=
(Ⅱ)第一局乙不出“剪刀”,则只能出“石头”或“布”,此时甲应该出“布”,才能保证不输给乙,甲胜的概率为 ;不妨设乙第一局出的“石头”,则乙第二局只能出“剪刀”或“布”,此时甲应出“剪刀”,才能保证不输给乙,则甲胜的概率为
;不妨设乙第一局出的“石头”,则乙第二局只能出“剪刀”或“布”,此时甲应出“剪刀”,才能保证不输给乙,则甲胜的概率为 ;同理第三、四、五局甲胜的概率也为
;同理第三、四、五局甲胜的概率也为 .
.
X的可能取值为3,4,5
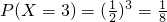 ,
,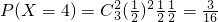 ,
,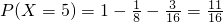
∴X的分布列为
故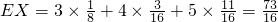
分析:(Ⅰ)根据“石头”胜“剪刀”,“剪刀”胜“布”,而“布”又胜“石头”,可得甲胜乙的概率;
(Ⅱ)先求第一局甲胜的概率为 ,同理第二、第三、四、五局甲胜的概率也为
,同理第二、第三、四、五局甲胜的概率也为 ,X的可能取值为3,4,5,求出相应的概率,即可得到X的分布列和期望.
,X的可能取值为3,4,5,求出相应的概率,即可得到X的分布列和期望.
点评:本题考查离散型随机变量的概率分布列与期望,解题的关键是确定X的可能取值,求出相应的概率.

(Ⅱ)第一局乙不出“剪刀”,则只能出“石头”或“布”,此时甲应该出“布”,才能保证不输给乙,甲胜的概率为
 ;不妨设乙第一局出的“石头”,则乙第二局只能出“剪刀”或“布”,此时甲应出“剪刀”,才能保证不输给乙,则甲胜的概率为
;不妨设乙第一局出的“石头”,则乙第二局只能出“剪刀”或“布”,此时甲应出“剪刀”,才能保证不输给乙,则甲胜的概率为 ;同理第三、四、五局甲胜的概率也为
;同理第三、四、五局甲胜的概率也为 .
.X的可能取值为3,4,5
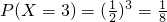 ,
,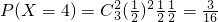 ,
,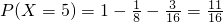
∴X的分布列为
| X | 3 | 4 | 5 |
| P |  |  | 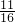 |
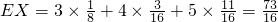
分析:(Ⅰ)根据“石头”胜“剪刀”,“剪刀”胜“布”,而“布”又胜“石头”,可得甲胜乙的概率;
(Ⅱ)先求第一局甲胜的概率为
 ,同理第二、第三、四、五局甲胜的概率也为
,同理第二、第三、四、五局甲胜的概率也为 ,X的可能取值为3,4,5,求出相应的概率,即可得到X的分布列和期望.
,X的可能取值为3,4,5,求出相应的概率,即可得到X的分布列和期望.点评:本题考查离散型随机变量的概率分布列与期望,解题的关键是确定X的可能取值,求出相应的概率.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目