题目内容
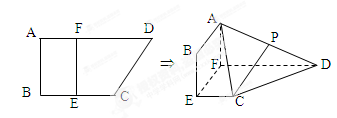
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为 ,构成一个三棱锥.
,构成一个三棱锥.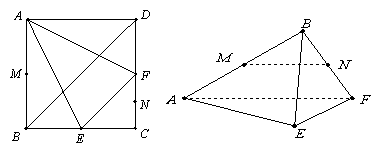
(1)请判断 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)证明 平面
平面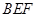 ;
;
(3)求二面角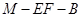 的余弦值.
的余弦值.
(1)平行;(2)证明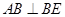 和
和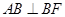 即可;(3)
即可;(3)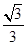
解析试题分析:本题考查空间想象能力,在折叠过程中,找到不变的量是求解的关键.(1)由中位线定理,可证明 平行
平行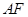 ;(2)证明
;(2)证明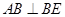 和
和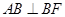 即可;(3)注意到三角形MEF、BEF都是等腰三角形,因此,取EF的中点即可求出二面角.
即可;(3)注意到三角形MEF、BEF都是等腰三角形,因此,取EF的中点即可求出二面角.
试题解析:(1) 平行平面
平行平面
证明:由题意可知点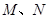 在折叠前后都分别是
在折叠前后都分别是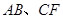 的中点(折叠后
的中点(折叠后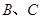 两点重合)
两点重合)
所以 平行
平行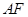 ,
,
因为 ,所以
,所以 平行平面
平行平面 .
.
(2)证明:由题意可知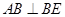 的关系在折叠前后都没有改变.
的关系在折叠前后都没有改变.
因为在折叠前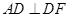 ,由于折叠后
,由于折叠后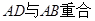 ,点
,点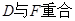 ,所以
,所以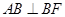
因为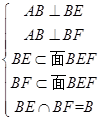 ,所以
,所以 平面
平面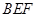 .
.
(3)解: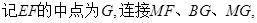
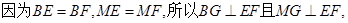
所以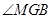 是二面角
是二面角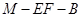 的平面角.
的平面角.
因为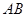 ⊥
⊥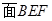 ,所以
,所以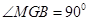 .
.
在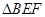 中,
中,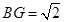 ,由于
,由于 ,所以
,所以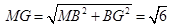 ,
,
于是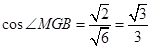 .
.
所以,二面角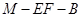 的余弦值为
的余弦值为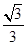 .
.
考点:1、线面平行;2、线面垂直的判定;3、二面角的概念及其求法.

练习册系列答案
相关题目
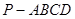 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱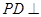 底面ABCD,
底面ABCD,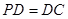 ,E是PC的中点.
,E是PC的中点.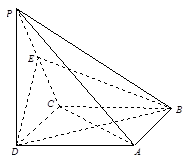
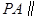 平面EDB;
平面EDB; 中,底面
中,底面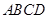 为平行四边形,侧面
为平行四边形,侧面 底面
底面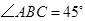 ,
,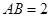 ,
,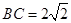 ,
,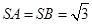 .
.
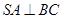 ;
;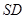 与平面
与平面 所成角的正弦值.
所成角的正弦值. 的底面为平行四边形,
的底面为平行四边形,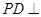 平面
平面 ,
, 为
为 中点.
中点.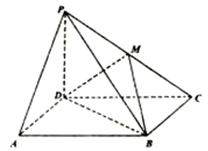
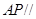 平面
平面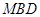 ;
;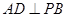 ,求证:
,求证: 平面
平面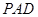 .
. 的底边
的底边 ,点
,点 在线段
在线段 上,
上, 于
于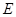 ,现将
,现将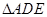 沿
沿 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
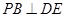 ;
; ,直线
,直线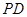 与平面
与平面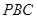 所成的角为
所成的角为 ,求
,求 长.
长. 所在平面与直角梯形ABCD所在平面互相垂直,
所在平面与直角梯形ABCD所在平面互相垂直, ,
, 点
点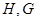 分别是线段
分别是线段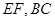 的中点.
的中点. 
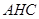
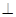 平面
平面 ;
;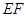 上是否存在点
上是否存在点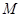 ,使得
,使得
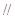 平面
平面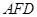 ,若存在,求
,若存在,求 的长并证明;若不存在,说明理由.
的长并证明;若不存在,说明理由.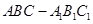 中,
中,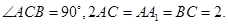

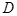 为
为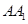 的中点,求证:平面
的中点,求证:平面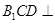 平面
平面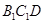 ;
;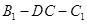 的大小为
的大小为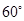 ,试确定
,试确定 中,
中,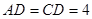 ,
, ,
, 是线段
是线段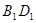 的中点.
的中点.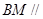 平面
平面 ;
;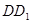 与平面
与平面
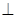 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.