题目内容
已知a为常数,则使得a>
dx成立的一个充分而不必要条件是( )
| ∫ | e 1 |
| 1 |
| x |
分析:由定积分计算公式,求出函数f(x)=
的一个原函数F(x)=lnx,从而利用微积分基本定理得到
dx=lne,结合充分条件、必要条件的定义,即可得到不等式成立的一个充分而不必要条件.
| 1 |
| x |
| ∫ | e 1 |
| 1 |
| x |
解答:解:由积分运算法则,得
dx=lnx
=lne-ln1=1
因此,不等式即a>
dx即a>1,对应的集合是(1,+∞)
将此范围与各个选项加以比较,只有C项对应集合(e,+∞)是(1,+∞)的子集
∴原不等式成立的一个充分而不必要条件是a>e
故选:C
| ∫ | e 1 |
| 1 |
| x |
| | | e 1 |
因此,不等式即a>
| ∫ | e 1 |
| 1 |
| x |
将此范围与各个选项加以比较,只有C项对应集合(e,+∞)是(1,+∞)的子集
∴原不等式成立的一个充分而不必要条件是a>e
故选:C
点评:本题给出关于定积分的一个不等式,求使之成立的一个充分而不必要条件,着重考查了定积分计算公式和充要条件的判断等知识,属于基础题.

练习册系列答案
相关题目
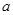 为常数,则使得
为常数,则使得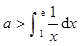 成立的一个充分而不必要条件是 ( )
成立的一个充分而不必要条件是 ( )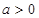 B.
B.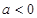 C.
C.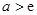 D.
D.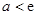
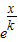 的一个承托函数,记实数a的取值范围为集合M,则有( )
的一个承托函数,记实数a的取值范围为集合M,则有( )