题目内容
若关于 的方程
的方程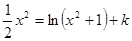 有四个不相等的实根,则实数
有四个不相等的实根,则实数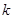 的取值范围是( )
的取值范围是( )
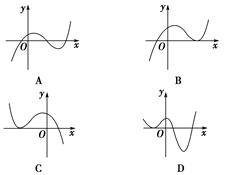
A.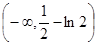 | B. | C.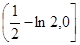 | D.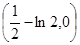 |
D
解析试题分析:令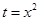 ,则
,则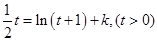 需要有两个不等正根,在同一平面直角坐标系中画出函数
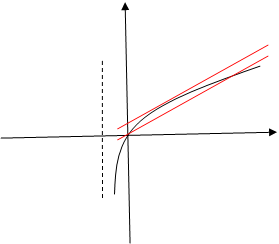
需要有两个不等正根,在同一平面直角坐标系中画出函数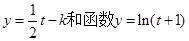 的图像,由图像知:当直线介于图中两条直线之间时(一条过原点,一条相切)满足题意,把原点代入得k=0;令
的图像,由图像知:当直线介于图中两条直线之间时(一条过原点,一条相切)满足题意,把原点代入得k=0;令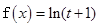 ,则
,则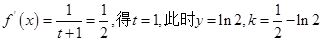 ,所以实数
,所以实数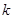 的取值范围是
的取值范围是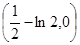 。
。
考点:函数与方程思想的综合应用;根的存在性及根的个数的判断。
点评:本题主要考查函数与方程的综合运用,及利用数形结合的思想研究方程根的问题。还考查了方程的根与函数零点的关系,属于中档题.做本题的关键是正确、快速画出函函数图像。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知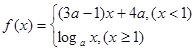 是(-
是(-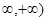 上的减函数,
上的减函数,
那么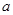 的取值范围是( )
的取值范围是( )
A.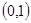 | B.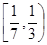 | C.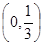 | D. |
若函数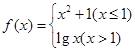 ,则
,则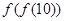 =( )
=( )
| A.lg101 | B.2 | C.1 | D.0 |
已知函数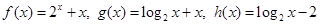 的零点依次为
的零点依次为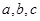 ,则( )
,则( )
A.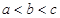 | B.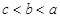 | C.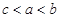 | D.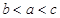 |
已知函数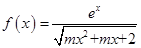 的定义域是
的定义域是 ,则实数
,则实数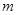 的取值范围是( )
的取值范围是( )
A.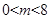 | B. | C. | D.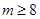 |
函数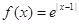 的单调递减区间是( )
的单调递减区间是( )
A.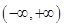 | B.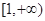 | C. | D.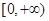 |
 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当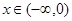 时,
时,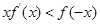 成立,若
成立,若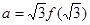 ,
,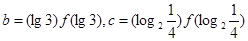 ,则
,则 大小关系( )
大小关系( )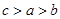
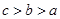
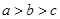
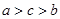
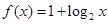 与
与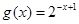 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )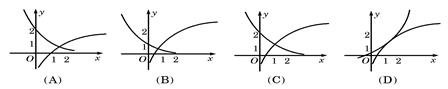
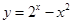 的图象大致是( )
的图象大致是( )