题目内容
给出下面四个条件:①
②
③
④
能使函数,y=1ogax-2为单调减函数的是
|
|
|
|
①④
①④
.(填上使命题正确的所有条件的代号)分析:令t=x-2,则y=1ogat,逐一分析满足题目中四个条件时,内外函数的单调性,并根据“同增异减”的原则,我们可以判断出复合函数y=1ogax-2的单调性,进而得到答案.
解答:解:令t=x-2,则y=1ogat,
则当
时,t=x-2为增函数,y=1ogat为减函数,则y=1ogax-2为单调减函数,故①满足条件;
当
时,t=x-2为减函数,y=1ogat为减函数,则y=1ogax-2为单调增函数,故②不满足条件;
当
时,t=x-2为增函数,y=1ogat为增函数,则y=1ogax-2为单调增函数,故③不满足条件;
当
时,t=x-2为减函数,y=1ogat为增函数,则y=1ogax-2为单调减函数,故④满足条件;
故答案为:①④
则当
|
当
|
当
|
当
|
故答案为:①④
点评:本题考查的知识点是对数函数的单调性与特殊点,其中熟练掌握对数函数,幂函数的单调性及复合函数单调性“同增异减”的原则,是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
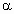 平行;
平行;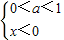 ②
②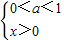 ③
③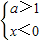 ④
④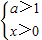 能使函数,y=1ogax-2为单调减函数的是 .(填上使命题正确的所有条件的代号)
能使函数,y=1ogax-2为单调减函数的是 .(填上使命题正确的所有条件的代号)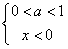 ,②
,②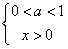 ,③
,③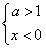 ,④
,④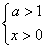 ,能使函数y=logax-2为单调减函数的是( )。
,能使函数y=logax-2为单调减函数的是( )。