题目内容
已知函数 (n∈Z)的图象与两坐标轴都无公共点,且其图象关于y轴对称,求n的值,并画出函数的图象.
(n∈Z)的图象与两坐标轴都无公共点,且其图象关于y轴对称,求n的值,并画出函数的图象.
 (n∈Z)的图象与两坐标轴都无公共点,且其图象关于y轴对称,求n的值,并画出函数的图象.
(n∈Z)的图象与两坐标轴都无公共点,且其图象关于y轴对称,求n的值,并画出函数的图象. 解:因为图象与y轴无公共点,所以n2-2n-3≤0,
又图象关于y轴对称,
则n2-2n-3为偶数,
由n2-2n-3≤0得,-1≤n≤3,
又n∈Z,∴n=0,±1,2,3,
当n=0或n=2时,y=x-3为奇函数,其图象不关于y轴对称,不适合题意;
当n=-1或n=3时,有y=x0,其图象如图A,
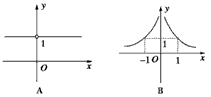
当n=1时,y=x-4,其图象如图B,
∴n的取值集合为{-1,1,3}.
又图象关于y轴对称,
则n2-2n-3为偶数,
由n2-2n-3≤0得,-1≤n≤3,
又n∈Z,∴n=0,±1,2,3,
当n=0或n=2时,y=x-3为奇函数,其图象不关于y轴对称,不适合题意;
当n=-1或n=3时,有y=x0,其图象如图A,

当n=1时,y=x-4,其图象如图B,
∴n的取值集合为{-1,1,3}.

练习册系列答案
相关题目