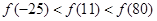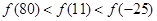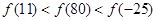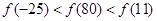题目内容
设f(x)=|x-1|-|x|,则f[f(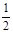 )]= ( )
)]= ( )
A.-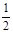 | B.0 | C.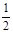 | D.1 |
D
解析

练习册系列答案
相关题目
若函数f(x)是定义在R上的偶函数,在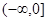 上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是 ( )
上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是 ( )
| A.(-¥,2) | B.(2,+¥) | C.(-¥,-2)È(2,+¥) | D.(-2,2) |
已知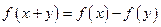 对于任意实数
对于任意实数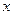 都成立,在区间
都成立,在区间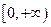 单调递增,
单调递增,
则满足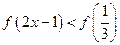 的
的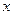 取值范围是 ( )
取值范围是 ( )
A.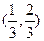 | B.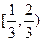  | C.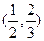 | D.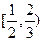 |
下列函数中,同时满足:有反函数,是奇函数,定义域和值域相同的函数是 ( )
A.y=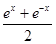 | B.y=lg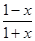 | C.y=-x3 | D.y=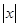 |
函数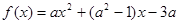 是定义在
是定义在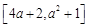 的偶函数,则
的偶函数,则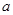 的值为 ( )
的值为 ( )
A.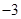 | B.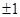 | C.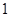 | D.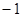 |
设函数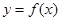 的反函数为
的反函数为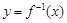 ,且
,且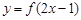 的图像过点
的图像过点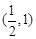 ,则
,则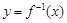 的图像必过 ( )
的图像必过 ( )
A.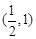 | B. | C.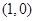 | D.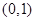 |
已知函数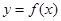 是R上的偶函数,且在(-∞,
是R上的偶函数,且在(-∞,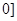 上是减函数,若
上是减函数,若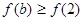 ,则实数a的取值范围是
,则实数a的取值范围是
| A.b≤2 | B.b≤-2或b≥2 | C.b≥-2 | D.-2≤b≤2 |
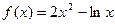 在其定义域的一个子区间
在其定义域的一个子区间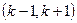 内不是单调函数,则实数
内不是单调函数,则实数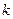 的取值范围是( )
的取值范围是( )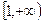
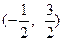
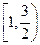
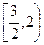
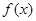 ,满足
,满足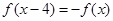 ,且在区间[0,2]上是增函数,则( ).
,且在区间[0,2]上是增函数,则( ).