题目内容

【题目】数列{an}满足2nan+1=（n+1）an ， 其前n项和为Sn ， 若 ，则使得 最小的n值为（ ）
A.8
B.9
C.10
D.11

【答案】D
【解析】解：∵2nan+1=（n+1）an ， ∴ = ，
若 ，
可得 = （ ）n﹣1=（ ）n ，
即有an=n（ ）n ，
前n项和为Sn=1（ ）1+2（ ）2+…+n（ ）n ，
Sn=1（ ）2+2（ ）3+…+n（ ）n+1 ，
两式相减可得， Sn=（ ）1+（ ）2+…+（ ）n﹣n（ ）n+1
= ﹣n（ ）n+1 ，
化简可得Sn=2﹣（n+2）（ ）n ，
则 即为（n+2）（ ）n＜ n（ ）n ，
化简可得n＞10，
则n的最小值为11．
故选：D．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系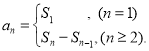才能正确解答此题．

练习册系列答案
相关题目

【题目】已知函数f（x）=exlnx（x＞0），若对 使得方程f（x）=k有解，则实数a的取值范围是（ ）
A.（0，ee]
B.[ee ， +∞）
C.[e，+∞）
D.

【题目】已知 ，函数 .
（1）当 时，解不等式 ；
（2）若关于 的方程 的解集中恰好有一个元素，求 的取值范围；
（3）设 ，若对任意 ，函数 在区间 上的最大值与最小值的差不超过1，求 的取值范围.

【题目】下列函数既是奇函数，又在间区 上单调递减的是( )
A.
B.
C.
D.

【题目】已知的顶点坐标为，，， 点P的横坐标为14，且，点是边上一点，且.

（1）求实数的值及点、的坐标；

（2）若为线段（含端点）上的一个动点，试求的取值范围.

【题目】已知函数f（x）=2sin（ωx+）﹣1（ω＞0，|φ|＜π）的一个零点是 ，其图象上一条对称轴方程为 ，则当ω取最小值时，下列说法正确的是 ． （填写所有正确说法的序号） ①当 时，函数f（x）单调递增；
②当 时，函数f（x）单调递减；
③函数f（x）的图象关于点 对称；
④函数f（x）的图象关于直线 对称．

【题目】已知，函数.

（1）当时，解不等式；

（2）若关于的方程的解集中恰好有一个元素，求的取值范围；

（3）设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.

【题目】已知函数 ，a∈R．
（Ⅰ）当a∈[1，e2]时，讨论函数f（x）的零点的个数；
（Ⅱ）令g（x）=tx2﹣4x+1，t∈[﹣2，2]，当a∈[1，e]时，证明：对任意的 ，存在x2∈[0，1]，使得f（x1）=g（x2）．

【题目】已知圆 的有 条弦，且任意两条弦都彼此相交，任意三条弦不共点，这 条弦将圆 分成了 个区域，（例如：如图所示，圆 的一条弦将圆 分成了2（即 ）个区域，圆 的两条弦将圆 分成了4（即 ）个区域，圆 的3条弦将圆 分成了7（即 ）个区域），以此类推，那么 与 之间的递推式关系为： ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网