题目内容
双曲线虚轴的一个端点为M,两个焦点为F1、F2,∠F1MF2=1200,则双曲线的离心率为
.
| ||
| 2 |
| ||
| 2 |
分析:根据题意,设虚轴的一个端点M(0,b),结合焦点F1、F2的坐标和∠F1MF2=120°,得到c=
b,再用平方关系化简得c=
a,根据离心率计算公式即可得到该双曲线的离心率.
| 3 |
| ||
| 2 |
解答:解:设双曲线的
-
=1(a>0,b>0)
∵可得虚轴的一个端点M(0,b),F1(-c,0),F2(-c,0),
∴由∠F1MF2=120°,得c=
b
平方得c2=3b2=3(c2-a2),可得3a2=2c2,
∴c=
a,得离心率e=
=
=
故答案为:
| x2 |
| a2 |
| y2 |
| b2 |
∵可得虚轴的一个端点M(0,b),F1(-c,0),F2(-c,0),
∴由∠F1MF2=120°,得c=
| 3 |
平方得c2=3b2=3(c2-a2),可得3a2=2c2,
∴c=
|
| c |
| a |
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题给出双曲线两个焦点对虚轴一端的张角为120度,求双曲线的离心率.着重考查了双曲线的标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
双曲线虚轴的一个端点为M,两个焦点为F1、F2,∠F1MF2=120°,则双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从双曲线虚轴的一个端点看两个顶点的视角为直角,则双曲线的离心率为( )
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
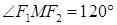 ,则双曲线离心率为
,则双曲线离心率为
 ,两个焦点为
,两个焦点为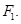
 ,
,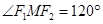 ,则双曲线的离心率为( )
,则双曲线的离心率为( )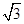 B、
B、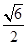 C、
C、 D、
D、